서 론
작물의 생산량을 증대시키기 위한 연구는 환경 요인의 영향을 정량화하여 생산량을 예측하거나, 원하는 작물 조직으로의 분배과정을 확인하는 등 다방면으로 진행되 고 있다(Heuvelink, 1996; Marcelis 등, 1998). 작물의 체내에서 일어나는 물질의 흐름은 광합성에 의한 동화 과정에서 시작하여 잎이나 줄기, 과실로 이동하는 형태 로 나타난다(Jones와 Tardieu, 1998; Prusinkiewicz, 1998). 이 중 광합성에 의한 동화 과정은 작물의 세포 내에서 일어나는 화학반응이므로, 광도와 온도, 이산화탄 소 농도 등의 환경 요인 의해 영향을 받아 증대되거나 감소한다(Kim과 Lieth, 2003; Caliskan 등, 2009). 환경 요인에 의한 광합성 속도 변화를 정량화 하려는 시도는 작물의 생산량을 예측하는 데 중요한 역할을 할 수 있 다. 최근에는 광합성에 영향을 미치는 환경 요인을 정량 화하는 연구 방법으로 모델링 기법이 각광받고 있다 (Medina-Ruíz 등, 2011; Noe와 Giersch, 2004).
광합성을 표현하는 모델은 그 형태가 간단한 것들이 많으나, 다양한 환경 요인에 대한 광합성 속도를 표현하 는 것에는 적절하지 않은 경우가 대부분이다. 이는 광합 성에 영향을 미치는 환경 요인이 극도로 다양하기 때문 이다(Johnson 등, 2010). 따라서 이런 문제를 해결하고자 기존에 단일 환경 요인에 대해 광합성 반응을 정량화 한 간단한 모델식을 서로 곱하여 만든 단순곱 모델이 주로 쓰여왔다. 단순곱 모델은 형태가 간단하여 광합성 반응에 대한 사전 지식 없이 단순한 두 식의 곱으로 구 성할 수 있으며 사용하기 편하다는 장점을 갖는다(Jones 등, 1991; Medina-Ruíz 등, 2011, Park 등, 2016). 그러 나 단순곱 모델은 작물의 생리적 현상 등을 반영하고 있지 않기 때문에 일반적으로 사용될 수 있는 모델이 아니다.
광도와 이산화탄소 농도에 대한 광합성 속도를 표현하 는 데에는 주로 직각쌍곡선(Rectangular hyperbola) 식이 나 음성지수(Negative exponential) 식이 쓰인다(Baker와 Allen, 1993; Valladares 등, 1997). 이 두 식은 광도나 이산화탄소 농도가 증가할 때 광합성 속도의 증가 속도 가 점차 줄어들어 포화되는 곡선의 형태를 표현하는 데 적합한 특성을 갖는다. Thornley (1974)는 광합성의 암 반응과 광반응에서 일어나는 화학적 반응에 대하여 간단 한 화학반응식을 작성하였다. 미분방정식의 형태로 표현 된 이 화학반응식을 정리하면 광합성 속도를 직각쌍곡선 식으로 표현하는 것이 가능해진다(Acock 등, 1976; Kaitala 등, 1982). 이 모델은 광도와 이산화탄소 농도의 변화에 따른 광합성 속도의 변화를 표현하는 데 적합하 지만, 온도나 생육 시기와 같은 변수에 대한 변화를 추 적하기에는 한계가 있다. 생육 시기가 진전됨에 따라 작 물의 형태가 변화하며 엽면적지수(LAI)가 변화하기 때문 에 작물의 각 부분에 도달하는 광도가 달라지게 된다 (Green, 1987). 또한 온도의 증가에 따라 식물체 내의 광합성 효소의 반응성이 달라지므로 온도에 따른 광합성 속도의 변화를 알아볼 필요가 있다. 따라서 기존의 직각 쌍곡선 모델식을 수정하면 다른 환경 요인의 작용을 표 현하는 데 적합할 것이다.
상추는 재배가 쉽고 식물공장 내에서의 재배법 등이 다양한 방면으로 연구되고 있는 모델 작물이다(Caporn 1989; Shimizu 등, 2008). 기존에 널리 사용되는 FvCB 모델은 여러 환경 변수에 의한 광합성 속도의 변화를 작물의 생리적 현상을 반영하여 표현했으나 특정 온도에 서 모델이 성립하도록 만들어진 특징을 가져 모델을 사 용하기 어려운 단점이 있다(Farquhar 등, 1980). 또한 장 미에 대하여 광도와 온도, 엽령으로 나타낸 생육 시기의 3 변수를 포함하는 형태의 간략한 모델식이 제시되었으나 (Leith와 Pasian, 1990), 상추와 같은 엽채류에 대해 유사한 연구는 거의 이루어지지 않았다. 따라서 본 연구에서는 흑 로메인 상추의 군락 광합성에 대해 단순곱 모델과 수정된 직각쌍곡선 모델을 이용하여 광도와 온도, 생육 시기에 따 른 광합성 속도를 예측하는 것을 목표로 하였다.
재료 및 방법
1. 식물 재료 및 재배 조건
군락 광합성 속도를 측정하기 위하여 서울대학교 식물 공장 모듈에서 흑로메인 상추(Lactuca sativa L., cv. Asia Heuk Romaine)를 재배하였다. 재배 베드는 120 × 80 × 10cm 크기이며, 3개의 베드가 수직으로 40cm 간 격으로 세로로 배열되었다. 전기전도도(EC) 1.2dS·m-1로 야마자키 상추 양액을 식물체에 공급하여 담액식 수경으 로 재배하였다(Yamazaki, 1982). 재배상의 온도와 광도 는 24±1°C와 200±20μmol·m-2·s-1로 각각 설정하였으며, 광원은 적:청:백 8:1:1의 비율을 갖는 120 × 10cm 크기 의 바(bar) 타입 LED 광원(FGL-B1200, FC Poibe Co., Ltd., Yeongdeungpo, Korea)을 재배 베드로부터 30cm 높이에 8개를 일렬로 설치하여 사용하였다. 2014년 7월 24일에 파종한 후 3주 동안 육묘하였고, 총 103개체의 상추를 3개의 재배 베드에 나누어 정식하였다. 상추는 총 4주 동안 식물공장에서 재배하였으며, 재배 밀도는 0.25 × 0.25m(36plants/m2)로 하였다. 같은 재배 조건 하 에서 103개체의 상추를 다시 재배하였으며, 이 상추는 검증 실험에 사용하였다.
2. 군락 광합성 측정
정식 후 4, 7, 14, 21, 28일의 다섯 단계의 생육 시기 에 해당하는 상추를 밀폐형 아크릴 챔버(1.0 × 0.8 × 0.5m)에 넣어 군락 광합성 속도를 측정하였다. 각 생육 시기별로 상추는 24, 24, 12, 8, 8개체를 측정에 사용하였 으며 작물의 배치 간격을 재배조건과 동일한 0.25 × 0.25m(36plants/m2)로 설정하였다. 동일한 챔버 3대를 이용 하여 3반복 측정하였다. 챔버 내부의 상대습도는 75%로 유지하였으며, 온도는 19±0.77°C, 22±0.78°C, 25±0.80°C, 28±0.85°C로 3°C 간격으로 4개의 처리 하에 광합성 속 도를 측정하였다. 광원은 적:청:백 8:1:1의 비율을 갖는 LED 광원을 사용하여 작물 잎 최상단부에서 50, 200, 350, 500μmol·m-2·s-1의 광도를 갖도록 4 개의 처리를 달 리 하여 광합성 속도를 측정하였다. 챔버 내부의 초기 이산화탄소 농도는 2,000μmol·mol-1로 설정하였다. 챔버 내부의 이산화탄소 농도 변화는 적외선 가스분석기(LI- 840A, LI-COR, Lincoln, NE, USA)를 이용하여 측정하 였고, 데이터 로거(CR1000, Campbell Scientific, Logan, UT, USA)를 이용해 측정된 값을 1초 간격으로 저장하 였다. 챔버 내부의 이산화탄소 농도가 2,000μmol·mol-1 에서 100μmol·mol-1로 상추의 광합성에 의해 감소하는 데 걸리는 시간 동안 이산화탄소 농도의 변화율을 계산 하여 상추 군락의 광합성 속도로 환산하였다. 4주 동안 실험이 진행되는 각 생육 단계별로 지상부 생체중과 건 물중, 엽면적을 측정하였다. 각 생육 단계에서 측정된 상추의 엽면적을 이용하여 군락 광합성 속도를 엽 광합 성 속도의 단위인 μmolCO2·m-2·s-1로 변환하였다.
3. 3 변수 단순곱 모델 구성
광도와 온도, 생육 시기에 따른 광합성 속도에 대한 일반적인 1변수 모델식은 각각 직각쌍곡선과 이차곡선, 지수함수로 알려져 있다. 따라서 본 연구에서는 3변수 단순곱 모델을 만들기 위하여 다음의 식을 구성하였다.(1)
여기서, P는 광합성 속도(μmolCO2·m-2·s-1), I는 광량 (μmol·m-2·s-1), C는 이산화탄소 농도(μmol·mol-1), T는 온도(°C), t는 생육 시기(d), a ~ e는 회귀분석 결과로 얻을 수 있는 회귀계수, R은 호흡에 의한 이산화탄소 발 생 속도(μmolCO2·m-2·s-1)를 의미한다. 광도, 온도, 생육 시기에 따른 군락 광합성 속도 측정 결과를 이용하여 SPSS (IBM, New York, NY, USA) 통계 프로그램에서 비선형 회귀분석을 실시하였다.
4. 3 변수 수정된 직각쌍곡선 모델 구성
Acock 등(1976)이 정립하고 Kaitala 등(1982)이 보완 하여 만들어진 광합성 직각쌍곡선 모델은 다음과 같은 식으로 표현된다.
여기서, P는 광합성 속도(μmolCO2·m-2·s-1), I는 광량 (μmol·m-2·s-1), C는 이산화탄소 농도(μmol·mol-1), α는 광화 학 이용효율(photochemical efficiency, μmolCO2·mol-1), β 는 카르복실화 컨덕턴스(carboxylation conductance, s-1), R은 호흡에 의한 이산화탄소 발생 속도(μmolCO2·m-2·s-1) 를 의미한다(Thornley, 1974).
단순곱 모델에서와 같은 방식으로 광도에 따른 군락 광합성 속도 측정 결과를 이용하여 SPSS (IBM, New York, NY, USA) 통계 프로그램에서 비선형 회귀분석을 실시하였다. 비선형 회귀분석으로 얻어진 광화학 이용효 율과 카르복실화 컨덕턴스, 호흡에 의한 이산화탄소 발 생 속도를 온도와 생육 시기를 X와 Y 축으로 갖는 3차 원 공간상에 나타내었다. 광화학 이용효율은 온도와 생 육 시기를 변수로 하는 모델식으로 구성 된 기존의 연 구가 없기 때문에 다음과 같은 경험식을 선정하여 비선 형 회귀분석을 실시하였다.
여기서, α는 광화학 이용효율(photochemical efficiency, μmolCO2·mol-1), T는 온도(°C), t는 생육 시기(d), a1 ~ d1은 회귀분석 결과로 얻을 수 있는 회귀계수를 의미한 다. 마찬가지로 카르복실화 컨덕턴스 또한 온도와 생육 시기를 변수로 하는 모델식으로 구성 된 기존의 연구가 없기 때문에 다음과 같은 경험식을 선정하여 비선형 회 귀분석을 실시하였다.(4)
여기서, β는 카르복실화 컨덕턴스(carboxylation conductance, s-1), T는 온도(°C), t는 생육 시기(d), a2 ~ e2은 회귀분석 결과로 얻을 수 있는 회귀계수를 의미한 다. 또한, 호흡에 의한 이산화탄소 발생 속도는 온도와 생육 시기에 따라 지수적으로 증가하므로(Lloyd와 Taylor, 1994), 아래와 같은 경험식을 구성하였다.
여기서, R은 호흡에 의한 이산화탄소 발생 속도 (μmolCO2·m-2·s-1), T는 온도(°C), t는 생육 시기(d), a3 ~ c3은 회귀분석 결과로 얻을 수 있는 회귀계수를 의미한 다. 광화학 이용효율과 카르복실화 컨덕턴스, 호흡에 의 한 이산화탄소 발생 속도를 각각 비선형 회귀분석을 실 시하여 회귀계수를 결정하였고, 그 결과로 얻어진 Eqs. 3 ~ 5를 Eq. 2에 대입하여 수정된 직각쌍곡선 모델을 구성하였다.
결 과
1. 생육 시기에 따른 지상부 생체중과 건물중, 엽면적
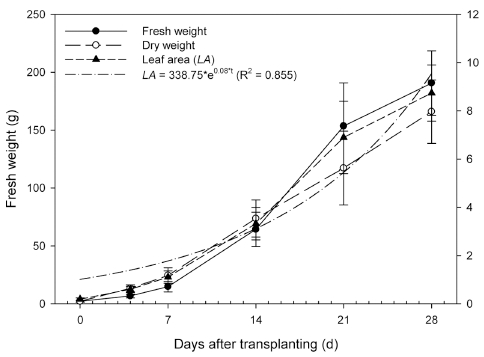
생육 시기가 진전됨에 따라 재배한 상추의 생체중과 건물중, 엽면적이 지수적으로 증가하였다(Fig. 1). 정식 후 28일차 상추의 생체중과 건물중, 엽면적은 각각 190.6±27.84g과 8.0±1.31g, 2912.5±389.31cm2으로 나타 났다. 엽면적(LA)의 경우 생육 시기를 변수로 하여 다음 과 같은 지수 모델을 따르는 것으로 회귀분석 되었다.
여기서, LA는 엽면적(cm2), t는 생육 시기(d)를 의미한다. 회귀분석 결과 Eq. 6의 R2 값은 0.855로 나타났다.
2. 3 변수 단순곱 모델 회귀분석 결과
온도와 광도를 X와 Y 축으로 하여 상추의 군락 광합 성 속도를 3차원 공간 상에 나타내었다(Fig. 2). 그림에 서 검은 점은 실제 측정을 통해 얻은 상추의 군락 광합 성 속도이며, 곡면은 단순곱 모델을 실험한 범위 내에서 나타낸 것이다. 곡면을 표현하는 단순곱 모델은 다음의 식으로 표현되었다.
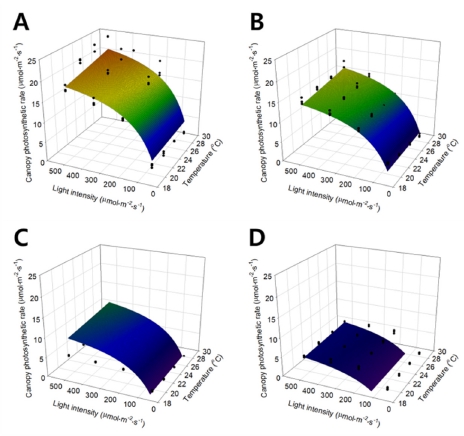
Fig. 2.
Canopy photosynthetic rates of the lettuces expressed with the simple multiplication model according to temperature and light intensity at 7 (A), 14 (B), 21 (C), and 28 (D) days after transplanting. Solid dots and curved meshes mean the canopy photosynthetic rates measured and regressed by simple multiplication model, respectively.
Eq. 7의 회귀분석 결과 R2 값은 0.852로 나타났다. 광 도가 증가함에 따라 군락 광합성 속도는 포화 곡선 형 태를 보이며, 온도가 증가함에 따라 광합성 속도는 지수 적으로 증가하는 양상을 나타내었다. 생육 시기에 따른 변화는 Fig. 2에서 시간 순으로 나열하였으며, A에서부 터 D까지 정식 후 7, 14, 21, 28일차 상추의 군락 광합 성 속도를 나타낸다. 생육 시기가 진전됨에 따라 군락 광합성 속도는 감소하는 것으로 나타났으나, 광도와 온 도에 따른 군락 광합성 속도 변화는 포화쌍곡선 형태를 유지하는 것으로 나타났다.
3. 3 변수 수정된 직각쌍곡선 모델 회귀분석 결과
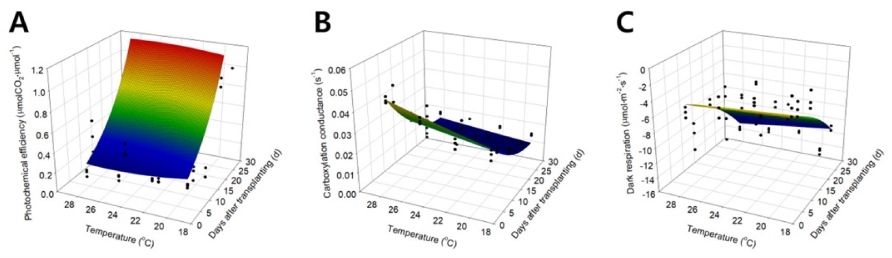
Eqs. 3 ~ 5로 표현된 광화학 이용효율과 카르복실화 컨덕턴스, 호흡에 의한 이산화탄소 발생 속도를 비선형 회귀 분석하여 얻은 회귀 계수를 Table 1에 나타내었다. Table 1의 각 회귀 계수를 Eqs. 3 ~ 5에 대입하여 광화 학 이용효율과 카르복실화 컨덕턴스, 호흡에 의한 이산 화탄소 발생 속도를 표현하는 곡면을 3차원 공간상에 나타냈다. 광화학 이용효율을 생육 시기와 온도를 X와 Y 축으로 하여 3차원 공간상에 나타내었을 때, 생육 시 기가 진전됨에 따라 광화학 이용 효율은 지수적으로 증 가하였으며 온도가 증가할 때 약 26°C에서 최대값을 갖 는 이차곡선의 형태로 나타났다(Fig. 3A). 카르복실화 컨덕턴스를 생육 시기와 온도를 X와 Y 축으로 하여 3 차원 공간 상에 나타내었을 때, 생육 시기가 진전됨에 따라 카르복실화 컨덕턴스는 지수적으로 감소하였으며 온도가 증가할 때 이차곡선을 따라 증가하였다(Fig. 3B). 호흡에 의한 이산화탄소 발생 속도를 생육 시기와 온도 를 X와 Y 축으로 하여 3차원 공간상에 나타내었을 때, 생육 시기가 진전됨에 따라 호흡에 의한 이산화탄소 발 생 속도는 지수적으로 감소하였으며 온도가 증가할 때 지수적으로 감소하였다(Fig. 3C).
Table 1. Regression coefficients and R2 values calculated using regression analysis in the modified rectangular hyperbola model.
단순곱 모델에서와 동일하게 온도와 광도를 X와 Y 축으로 하여 상추의 군락 광합성 속도를 3차원 공간 상 에 나타내었다(Fig. 4). 그림에서 검은 점은 실제 측정을 통해 얻은 상추의 군락 광합성 속도이며, 곡면은 수정된 직각쌍곡선 모델을 실험한 범위 내에서 나타낸 것이다. 곡면을 표현하는 수정된 직각쌍곡선 모델은 Table 1에 표기된 a, b, R의 회귀분석 결과를 이용하여 하나의 식 으로 표현되었다.
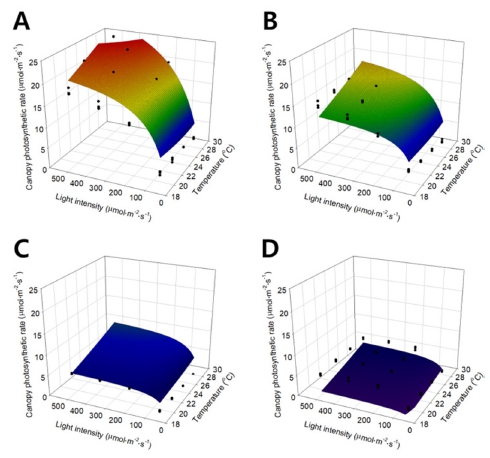
Fig. 4.
Canopy photosynthetic rates of the lettuces expressed with the modified rectangular hyperbola model according to temperature and light intensity at 7 (A), 14 (B), 21 (C), and 28 (D) days after transplanting. Solid dots and curved meshes mean the canopy photosynthetic rates measured and regressed by the modified rectangular hyperbola model, respectively.
광도가 증가함에 따라 군락 광합성 속도는 포화 곡선 형태를 보이며, 온도가 증가함에 따라 광합성 속도는 지 수적으로 증가하는 양상을 나타내었다. 생육 시기에 따 른 변화는 Fig. 4에서 시간 순으로 나열하였으며, A에서 부터 D까지 정식 후 7, 14, 21, 28 일차 상추의 군락 광합성 속도를 나타낸다. 생육 시기가 진전됨에 따라 군 락 광합성 속도는 감소하는 것으로 나타났으나, 광도와 온도에 따른 군락 광합성 속도 변화의 양상은 유지되는 것으로 나타났다.
4. 단순곱 모델과 수정된 직각쌍곡선 모델 검증 결과
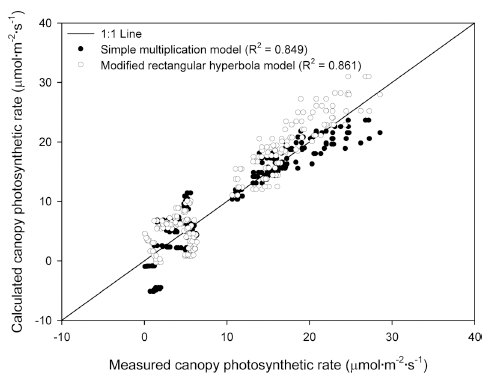
단순곱 모델과 수정된 직각쌍곡선 모델을 이용하여 계 산한 상추의 군락 광합성 속도와 실험을 통해 측정된 군락 광합성 속도를 1:1 선상에서 회귀분석을 수행하였 을 때, 두 모델에서의 검증 R2 값에서 0.012의 차이가 나타났다(Fig. 5). 단순곱 모델의 검증 결과 R2 값은 0.849로 나타났으며, 수정된 직각쌍곡선 모델의 검증 결 과 R2 값은 0.861로 단순곱 모델에 비해 소폭 높은 것 으로 나타났다.
고 찰
단위 엽면적 당 이산화탄소의 흡수량은 엽 광합성 속 도를 나타내는 데 주로 사용되는 단위이다. 그러나 여러 개체의 작물이 군락을 형성하고 있는 경우에는 군락 광 합성 속도를 개체 당 이산화탄소 흡수량으로 표현할 필 요가 있다. Eq. 6에 표현된 엽면적 모델을 이용하면 작 물 개체 당 이산화탄소 흡수량으로 표현된 군락 광합성 속도를 단위 엽면적 당 이산화탄소의 흡수량으로 표현되 는 엽 광합성 속도와 같은 단위로 변환할 수 있다. 따라 서 엽면적 모델은 군락 광합성 속도를 엽 광합성 속도 와 비교하기 위해 필요한 선행 모델이라 할 수 있다.
광합성 속도의 측정을 위해서는 다양한 형태의 챔버가 사용되고 있다(Mitchell, 1992). 여러 형태의 챔버들 중 밀폐형 챔버는 군락 광합성 측정을 위해 사용할 수 있 다. 밀폐형 챔버는 구조가 단순하다는 장점이 있으나, 정상 상태의 광합성 속도를 측정하기 어렵다는 단점을 갖는다(Bugbee, 1992). 직각쌍곡선 모델은 광합성의 반 응에 대해 미분방정식 형태로 구성된 것이므로 동적 모 델의 한 형태이다(Thornley, 1974). 따라서 본 연구에 사 용한 동적 모델인 직각쌍곡선 모델은 밀폐형 챔버를 이 용해 군락 광합성 속도를 측정하고 표현하는 데 적합한 모델이라 할 수 있다.
광도 220μmol·m-2 정도에서 버드나무를 이용한 기존 연구에 따르면, 광화학 이용효율과 카르복실화 컨덕턴스 값은 0.00028μmol-1·m2과 0.001053(kg·CO2·m-3)·s-1로 나 타났다(Kaitala 등, 1982). 또한 Atriplex hastata 종에서 측정된 광화학 이용효율은 0.177μmolCO2·μmol-1로 알려 졌다(Marshall과 Biscoe, 1980). 그러나 기존의 연구들 중에서 온도와 생육 시기가 변함에 따라 광화학 이용효 율과 카르복실화 컨덕턴스가 어떻게 변화하는 지 추적한 경우는 없었다. 본 연구에서는 광화학 이용효율과 카르 복실화 컨덕턴스가 온도와 생육 시기가 변화함에 따라 어떤 변화를 보이는 지 추적하여 모델을 구성하였다. 장 미에서 광도와 온도, 엽령으로 표현된 생육 시기를 변수 로 하는 광합성 속도 모델에서는 광화학 이용효율과 카 르복실화 컨덕턴스의 변화는 추적하지 않았다(Leith와 Pasian, 1990). 이는 다른 종의 작물에서도 광화학 이용 효율과 카르복실화 컨덕턴스의 변화를 추적할 필요가 있 음을 시사하며, 작물의 생리적 현상을 반영한 모델로 수 정된 직각쌍곡선 모델이 유용하다는 것을 의미한다.
단순곱 모델과 수정된 직각쌍곡선 모델을 비교하는 관 점에서 회귀분석 결과인 R2 값을 비교할 수 있다. 단순 곱 모델은 회귀계수를 한 번의 비선형 회귀분석을 통해 얻을 수 있었으며, 식 7에서 R2 값은 0.852로 나타났다. 반면, 수정된 직각쌍곡선 모델은 두 번의 비선형 회귀분 석이 수행된다. α, β, R의 회귀분석 결과, 각각 R2 값이 0.741, 0.849, 0.635로 나타났다(Table 1). 이는 α, β, R 각각의 회귀분석에서 단순곱 모델에 비해 낮은 정확도를 나타내는 것으로 보이나, 최종적으로 완성된 수정된 직 각쌍곡선 모델은 검증 과정에서 R2 값이 0.861로 단순 곱 모델의 0.849에 비해 높게 나타나는 역전 현상을 보 인다. 본 연구에서는 α, β, R의 모델식을 경험적으로 구 성하였으나, 후속 연구를 통해 더 높은 정확도를 갖는 식을 찾게 된다면 검증 결과에서 큰 차이를 보일 수 있 을 것으로 판단된다.
본 연구에서는 광량과 온도, 생육 시기의 3변수를 포 함하는 광합성 모델을 찾고자 하였다. 광합성에 영향을 미치는 요인들이 다양하다는 것은 널리 알려진 사실이지 만, 실제로 모든 환경 요인들을 포함하는 모델을 구축하 는 데에는 어려움이 따르기 때문에 추정이 쉬운 1변수 혹은 2변수 모델들이 주로 사용되고 있었다(Larsen, 1990). 3변수 이상의 모델은 각 요인의 상호작용 등을 고려하여 모델을 확립해야 하므로 구축이 어렵다. 최근 활발한 연구가 진행중인 인공신경망(Artificial Neural Network) 분야의 기술을 광합성 모델을 구축하는 데 적 용한다면, 3변수 이상의 조건에서도 모델을 활용할 때보 다 정확한 결과를 얻을 수 있을 것이다(Vaidyanathan 등, 2015; Taormina와 Chau, 2016). 그러나 군락 광합성 속 도 모델을 확립하는 것은 인공신경망 방식을 사용하기 위해 요구되는 많은 양의 데이터를 습득하기 전 단계에 서 유리할 것으로 판단된다. 또한 작물의 광합성을 표현 하는 수식으로 모델이 정립되어 있으므로 연구자와 실제 작물을 재배하는 농민 등이 유용하게 사용할 수 있을 것이다.