Performance Evaluation of a Reference Evapotranspiration Model in Reclaimed Land Environments and Comparison with Inland Areas

Junwoo Moon; Haksung Lee; Joonwoo Lee

doi:10.12791/KSBEC.2024.33.4.373

Preview

Original Articles

Journal of Bio-Environment Control. 31 October 2024. 373-386
https://doi.org/10.12791/KSBEC.2024.33.4.373

Performance Evaluation of a Reference Evapotranspiration Model in Reclaimed Land Environments and Comparison with Inland Areas

간척지 지역의 기준 작물 증발산 모델 성능 평가 및 내륙지역과의 증발산 비교

Junwoo Moon¹

Haksung Lee²

Joonwoo Lee³⁴^*

문 준우¹

이 학성²

이 준우³⁴^*

¹Graduate Student, Department of Agricultural Engineering, College of Agricultural & Life Sciences, Jeonbuk National University, Jeonju 54896, Korea

²Researcher, Reclaimed Land Agriculture Research Team, National Institute of Crop Science, RDA, Wanju 55365, Korea

³Professor, Department of Smart Farm, Jeonbuk National University, Jeonju 54896, Korea

⁴Professor, Department of Agricultural Engineering, College of Agricultural & Life Sciences, Jeonbuk National University, Jeonju 54896, Korea

¹전북대학교 농업생명과학대학 농공학과 대학원생

²국립식량과학원 간척지농업연구팀 연구사

³전북대학교 스마트팜학과 교수

⁴전북대학교 농업생명과학대학 농공학과 교수

^{*Corresponding Author}

ABSTRACT

In South Korea, reclaimed lands, covering approximately 130,000 ha, are utilized as agricultural hubs. Recently, there has been a trend of converting paddy fields to upland fields, highlighting the increasing importance of agricultural water supply. Although there has been extensive research on crop growth in reclaimed land environments, studies on irrigation quantity estimation for such lands are limited. Therefore This study aimed to estimate appropriate irrigation quantities for the unique climatic conditions of reclaimed land by analyzing and evaluating five reference evapotranspiration (ET_o) models, and then comparing them with inland region climates. By applying climate data from the Saemangeum reclaimed land to models, and comparing ET_o values calculated by these models with actual ET_o values measured using lysimeters, it was found that FAO Penman-Monteith equation exhibited the highest accuracy with a root mean square error (RMSE) of 1.36. However, it showed almost similar accuracy to Priestley-Taylor equation, which had an RMSE of 1.38. The climates of Saemangeum and Jeonju differed in wind speed and humidity. When applying FAO Penman-Monteith and Priestley-Taylor equations, which showed high performance, to both regions, the results showed that FAO Penman-Monteith equation had an R² of 0.70, while Priestley-Taylor equation had an R² of 0.90. The difference in ET_o between the two regions was attributed to FAO Penman-Monteith equation reflecting the differences in wind speed between Saemangeum and Jeonju. Therefore, FAO Penman-Monteith equation is considered the most suitable model for reclaimed land, while Priestley-Taylor equation may also be appropriate when data on wind speed and humidity are difficult to obtain.

Keywords

FAO Penman-Monteith

irrigation

lysimeter

reference crop

saemangeum

본 연구는 간척지의 특수한 기후 조건에서 적합한 관수량을 산정하기 위해 5가지 기준 증발산 모델을 분석 및 평가한 후, 내륙지역 기후에 적용해 비교하였다. 새만금 간척지의 기후 데이터를 모델에 적용한 기준 증발산량과 라이시미터로 측정한 실제 기준 증발산량을 비교한 결과 FAO Penman-Monteith 방정식이 평균 제곱근 편차 RMSE가 1.36으로 가장 높은 정확도를 보였으나 RMSE가 1.38인 Priestley-Taylor 방정식과 거의 유사한 정확도를 보였다. 새만금과 전주의 기후는 풍속과 습도가 상이하였고, 높은 성능을 보인 FAO Penman-Monteith 방정식과 Priestley-Taylor 방정식을 두 지역에 적용하였다. 그 결과, FAO Penman-Monteith 방정식은 R² = 0.70, Priestley-Taylor 방정식은 R² = 0.90이었다. 두 지역에 대한 두 모델의 기준 증발산량 차이는 FAO Penman-Monteith 방정식이 새만금과 전주의 풍속 차이를 반영했기 때문으로 판단된다. 따라서 풍속을 반영한 FAO Penman-Monteith 방정식이 간척지에 가장 적합한 모델로 판단되며, 풍속과 습도의 데이터 측정이 어려울 경우 Priestley-Taylor 방정식의 사용도 적합할 것으로 보인다.

키워드

관수

기준 작물

라이시미터

새만금

FAO Penman-Monteith

MAIN

서 론
재료 및 방법
1. 기상 데이터 수집
2. 간척지 기준 증발산량 측정
3. 간척지에서의 최적 기준 증발산 모델 성능 평가
4. 간척지 및 내륙지 기준 증발산 비교 시뮬레이션
5. 통계방법
결과 및 고찰
1. 간척지와 내륙지역 기후 비교
2. 간척지 기준 증발산량 측정
3. 간척지 기후에서의 적합한 기준 증발산 모델 성능 평가
4. 간척지와 내륙지역 기준 증발산량 비교

서 론

국내 간척지는 130,000ha에 달하는 면적으로 농업 단지 거점으로 활용되고 있다. 이러한 농업 단지에서 농업용수 시설은 수확량과 농업소득 증가 등 중요한 요소이지만(FAO, 2024), 간척지 토양은 기존의 내륙 재배지와 다르게 지하수위가 높아 배수가 불량하여 염분 집적이 쉬워 내륙 재배지와 다른 관수 체계를 수립해야 한다(Kim 등, 2011). 농림축산식품부와 한국농어촌공사는 농생명 용지 조성에 맞추어 농업용수 공급의 필요성을 강조하였다(KDI, 2023). 최근에는 간척지의 논 재배가 밭 재배지로 전환되는 추세이며, 이러한 농업용수 공급 방식 변경에 따라 관수 체계에 대한 연구 필요성이 대두되고 있다(Kang 등, 2023).

간척지에 대한 연구는 다양한 측면에서 진행되었다. 예를 들어 Jeong 등(2020)은 간척지 토양의 토성과 염분을 분석하여 재배에 적합한 작물을 결정하는 연구를 수행하였고, Kim 등(2016), Abbady 등(2021), 그리고 Oh 등(2022)은 높은 염분과 같은 환경적 스트레스가 식물에 미치는 영향을 분석하였다. 또한 Ryu 등(2020)은 간척지의 근권부에서 증발산량을 추정하여 재염화 억제를 위한 관수법을 연구했으며, Bae 등(2015)과 Lee 등(2021)은 관수 시 염분 농도에 관한 연구를 진행하였다. 하지만 간척지의 특수한 기후에서 적합한 관수량 기준에 대한 체계적인 접근은 미흡하였다. 기존 간척지 연구에서는 작물의 권장 관수량을 산정하거나 모델을 사용해 추정하는 방법이 적용되어 왔다. 그러나 이러한 산정 방식에 대한 검증이 부족하며, 실제 재배 환경에서 적절한 관수량을 구체적으로 제시한 연구는 여전히 부족한 실정이다.

관수량 산정에는 다양한 방법이 있으며, 그중 FAO 증발산량을 통한 관수량 산정 방법을 널리 사용한다(Allen 등, 1998). FAO 방법에 따르면 표준 조건 하에서의 증발산량(ET_c)은 기후의 영향을 받는 기준 증발산량(ET_o)과 작물 및 생육단계의 영향을 받는 작물계수(K_c)로 산정할 수 있는데, 이때 ET_o는 세계적으로 널리 사용되는 표준 방법으로 넓은 범위의 기후와 지역에서 정확히 예측할 수 있는 FAO Penman-Monteith 방정식부터 온도 값만으로 증발산을 예측할 수 있는 Hargreaves 방정식까지 다양한 기준 증발산 모델이 있다(Fazlil-Ilahil, 2009; Liu 등, 2017; Prenger 등, 2002).

증발산에는 일사량, 온도, 습도, 풍속, 기압 등 여러가지 환경 변수가 영향을 미치며(Allen 등, 1998; Zhao 등, 2023), 국내 간척지는 내륙지역의 기후와 상이하기 때문에(Hah와 Lee, 2014; Nam과 Shin, 2017) 이를 분석하고 적합한 증발산 모델을 사용하도록 해야 한다. 따라서 본 연구는 간척지 기후에서 적합한 기준 증발산 모델로 재배 관수량 산정하기 위해 기준 증발산 모델의 성능을 평가하였다. 이를 위해 새만금 간척지와 내륙지역인 전주의 기후를 측정하여 간척지의 기후 특성을 분석하였고, 새만금 간척지 기후를 적용한 5개의 증발산 모델을 시뮬레이션 하여 성능을 평가 하였다. 그중 높은 성능을 보인 모델은 내륙지역 재배지 기후에 적용하여 간척지와의 기준 증발산량을 비교하였다.

재료 및 방법

1. 기상 데이터 수집

간척지의 데이터는 전북특별자치도 새만금(35° 83'N 126° 68'E, 2m)에서 기상 센서(ATMOS 41W, Meter Group Inc., Pullman, WA, USA)를 사용하여 2023년 5월 24일부터 2024년 7월 7일까지 15분 간격으로 일사량(W·m^-2), 온도(°C), 상대습도(%), 풍속(m·s^-1), 기압(kPa)을 측정하여 분석하고 기준 증발산 모델에 적용하였다.

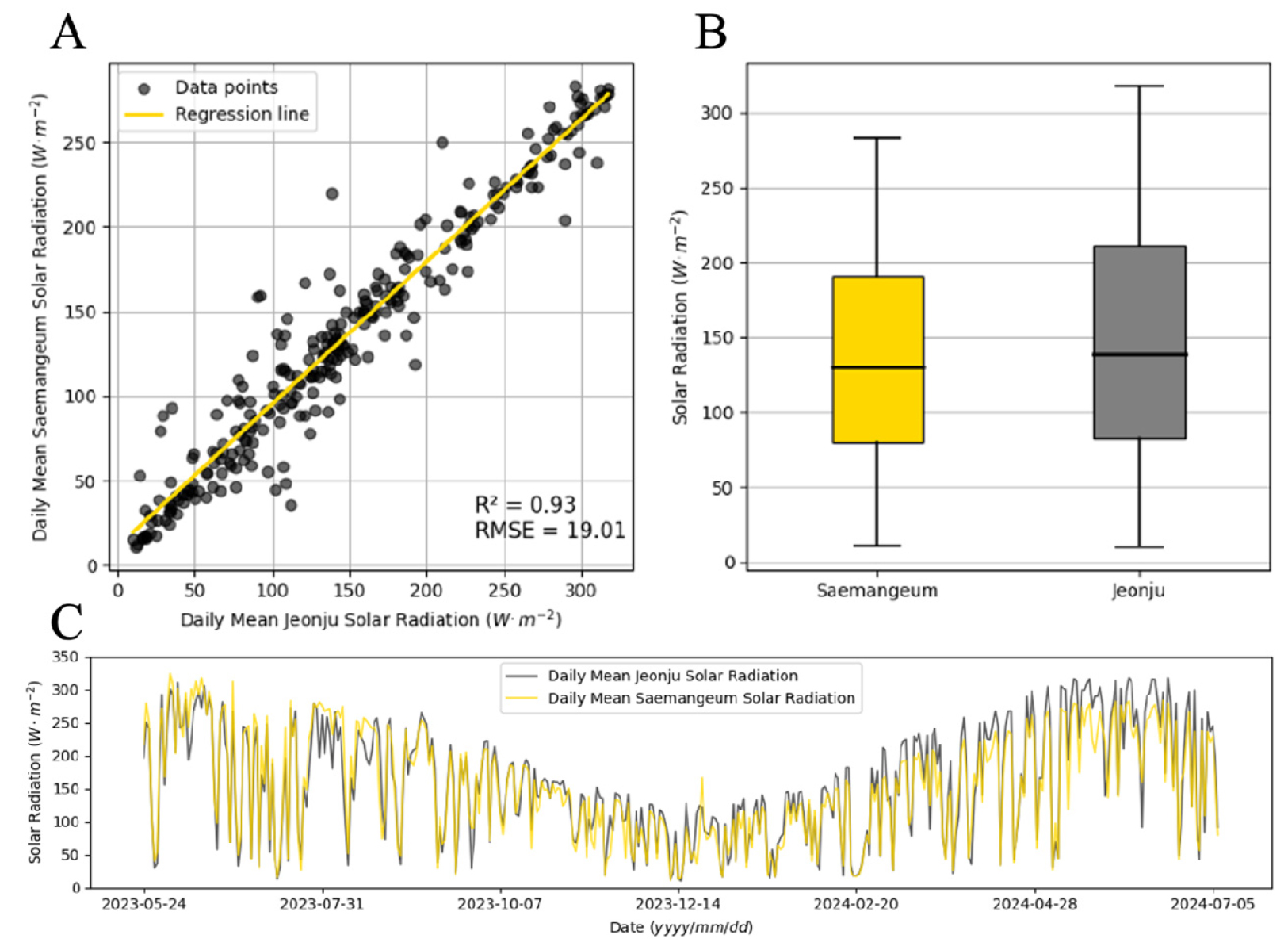
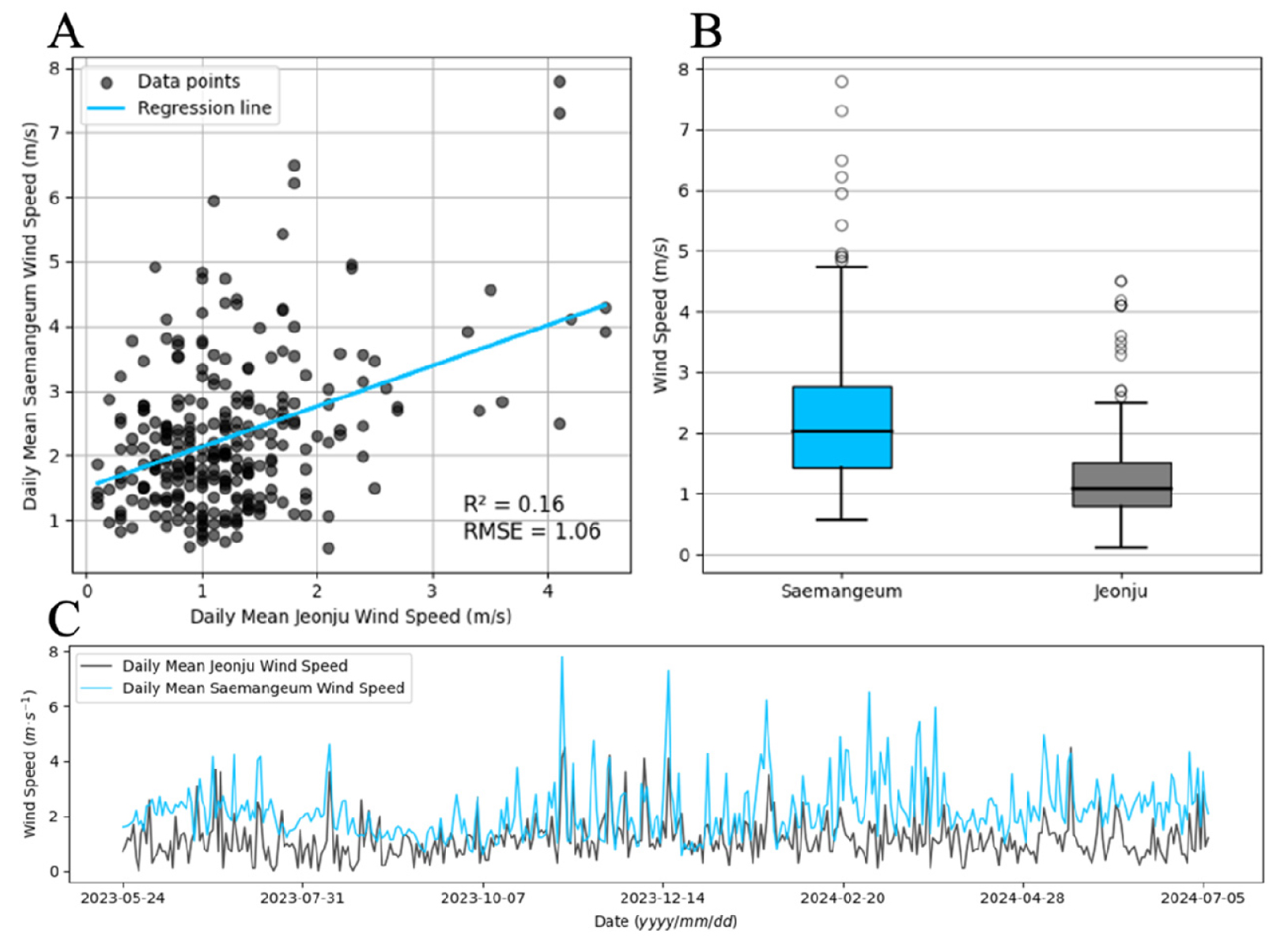
새만금 간척지 지역의 기준 증발산 특성과 내륙지역의 증발산 특성을 비교하기 위해 내륙지역인 전주시 기상 데이터를 수집하였다. 내륙지역의 기상 데이터는 기상청 기상자료개방포털 종관기상관측(ASOS)에서 전북특별자치도 전주시(35° 50' 27"N 127° 07' 00"E, 50m)의 2023년 5월 24일부터 2024년 7월 7일까지 1시간 간격으로 일사량(W·m^-2), 온도(°C), 상대습도(%), 풍속(m·s^-1), 기압(kPa)을 수집하여 새만금 간척지 기후와 비교하였다(Fig. 1 A).

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F1.jpg

Fig. 1.

Weather sensor ATMOS 41W (Meter Group Inc., Pullman, WA, USA) (A) and lysimeter (BWL-LY500, Hanul, Daejeon, South Korea) (B) installed in Saemangeum.

2. 간척지 기준 증발산량 측정

모델 선정을 위한 실제 기준 증발산량 측정은 0.12m에서 0.15m인 잔디가 심어진 두 개의 라이시미터(BWL-LY500, Hanul, Daejeon, South Korea)로 측정하였다(Fig. 1B). 라이시미터 데이터는 2023년 9월 21일부터 2024년 6월 27일까지 10분 간격으로 ET_o 값을 측정하여 사분범위(interquartile range; IQR) 통계 방법을 통해 이상치를 제거하고 하루 기준 증발산량을 계산하였으며, 두 증발산량의 값 차이가 절댓값 1보다 큰 날은 제거하였다. 또한, 강수일과 전날보다 무게가 증가한 날의 데이터를 제외하였다.

3. 간척지에서의 최적 기준 증발산 모델 성능 평가

모델 시뮬레이션에 사용한 기후 데이터는 일평균 일사량(W·m^-2), 상대습도(%), 풍속(m·s^-1), 기압(kPa), 온도(°C)와 일 최고, 최저 온도(°C)이다. 순 복사량을 사용하는 모델에는 일사량(W·m^-2)을 순 복사량(MJ·m^-2·day^-1)으로 변환하였고(Katsoulas와 Stanghellini, 2019), 대기 외 일사량(MJ·m^-2·day^-1)은 연중 일수와 위도를 통해 계산하였다(Allen 등, 1998). 각 모델에 사용되는 내부 저항과 외부 저항값은 70s·m^-1과 50s·m^-1로 고정하였다(Prenger 등, 2002; Oke, 2002). 새만금 기후에 적합한 증발산 모델 사용을 위한 성능 평가는 에너지 밸런스 기반인 FAO Penman-Monteith 방정식(Allen 등, 1998), Simplified 방정식(Baille 등, 1994), Fynn 방정식(Prenger 등, 2002), 일사량 기반인 Prestley-Taylor 방정식(Priestley와 Taylor, 1972), 온도 기반인 Hargreaves 방정식(Hargreaves와 Samani, 1985)으로 총 5개 모델을 사용하였다(Tables 1, 2).

새만금 간척지 증발산량의 비교는 라이시미터 측정일을 기준으로 각 기준 증발산 모델 시뮬레이션 값을 비교하였다. 라이시미터 실측값에 대한 기준 증발산 모델의 정확도 성능 지표는 평균 제곱근 편차(RMSE)를 계산하였다.

Table 1.

Five Reference Evapotranspiration (ET_o) models used for predicting evapotranspiration in Saemangeum.

	ET_o Model	Equation
Combination method based on energy balance	FAO Penman - Monteith (Allen et al., 1998)	$E T_{o} = \frac{0.408 ∆ (R_{n} - G) + γ \frac{900}{T + 273} u_{2} (e_{s} - e_{a})}{∆ + γ (1 + 0.34 u_{2})}$
	Simplified (Baille et al., 1994)	$E = A f_{1} (L) G + B f_{2} (L) D$ $f_{1} = 1 - \exp (- α L) A = \frac{∆}{∆ + γ^{}}$ $f_{2} = L B = \frac{1}{λ} [\frac{3.6 \times 10^{3} ρ C_{p} / r_{a}}{∆ + γ^{}}]$
	Fynn (Prenger et al., 2002)	$λ E = \frac{δ}{δ + γ^{}} C A I (R_{n} - G) + \frac{γ}{δ + γ^{}} 2 L A I ρ_{a} λ (e_{a}^{*} - e_{a}) + r_{e}$
Radiation based	Priestley-Taylor (Priestley and Taylor, 1972)	$E T_{o} = \frac{1}{λ} α \frac{∆}{∆ + γ} (R_{n} - G)$
Temperature based	Hargreaves (Hargreaves and Samani, 1985)	$E T_{o} = \frac{1}{λ} (0.0023) (T_{m e a n} + 17.8) (T_{\max} - T_{\min})^{0.5} R_{a}$

Table 2.

Definition and units of parameters used in each evapotranspiration model.

Term	Unit	FAO P-M	Simplified	Fynn	P-T	Hargreaves
Reference Evapotranspiration	mm·day^-1	$E T_{o}$	$E$	$E$	$E T_{o}$	$E T_{o}$
Net Radiation	MJ·m^-2·day^-1	$R_{n}$	$G (k g m^{- 2} h^{- 1})$	$R_{n}$	$R_{n}$	NA
Soil heat flux density	MJ·m^-2·day^-1	$G$	NA	$G$	$G$	NA
Extra-terrestrial solar radiation	MJ·m^-2·day^-1	NA	NA	NA	NA	$R_{a}$
Air vapour pressure deficit	kPa	$e_{s} - e_{a}$	$D$	$e_{a}^{*} - e_{a}$	NA	NA
Canopy area index, i.e., ratio if canopy area	m² m^-2	NA	NA	$C A I$	NA	NA
Density of air	kg m^-3	NA	$ρ$	$ρ_{a}$	NA	NA
Empirical coefficient of 1.26 (Kashyap and Panda, 2001; Liu et al., 2008)		NA	NA	NA	$α$	NA
Latent heat of vaporization of water	J kg1	NA	$λ$	$λ$	$λ$	$λ$
Leaf aerodynamic resistance		NA	$r_{a}$	$r_{e}$	NA	NA
Leaf angle distribution (0.64 from Stanghellini (1987))		NA	$α$	NA	NA	NA
Leaf area index (m² m^-2)	m² m^-2	NA	$L$	$L A I$	NA	NA
Maximum daily air temperature	°C	NA	NA	NA	NA	T_max
Mean daily air temperature	°C	$T$	NA	NA	NA	T_mean
Minimum daily air temperature	°C	NA	NA	NA	NA	T_min
Psychrometric constant	kPa °C^-1	$γ$	$γ^{*}$	$γ$	$γ$	NA
Slope vapor pressure curve	kPa °C^-1	$∆$	$∆$	$δ$	$∆$	NA
Specific heat of air	J kg^-1 K^-1	NA	$C_{p}$	NA	NA	NA
Wind speed at z (m) height	m·s^-1	$u_{2}$	NA	NA	NA	NA

NA = Not applicable or not used

4. 간척지 및 내륙지 기준 증발산 비교 시뮬레이션

새만금 기후와 내륙지역 기후에서 기준 증발산량을 비교하기 위해 ‘1. 기상 데이터 수집’에서 수집한 내륙지역의 기후 데이터를 ‘3. 간척지에서의 최적 기준 증발산 모델 성능 평가’에서 높은 성능을 보인 3가지 기준 증발산 모델에 적용하여 계산하였다. 이를 통해 새만금 간척지와 내륙지의 증발산량 양상에 대해 분석을 수행하였다.

5. 통계방법

모델 성능 평가에 사용된 통계방법은 Python 프로그램에서 Numpy 라이브러리를 사용하여 결정계수(R²), 피어슨 상관계수(R), 평균 제곱근 편차(RMSE)를 계산하였다. 또한 Hargreaves를 제외한 4가지 모델의 그룹 간 평균 차이를 분석하기 위해 일원분산분석(One-way ANOVA)을 사용하였다.

결과 및 고찰

1. 간척지와 내륙지역 기후 비교

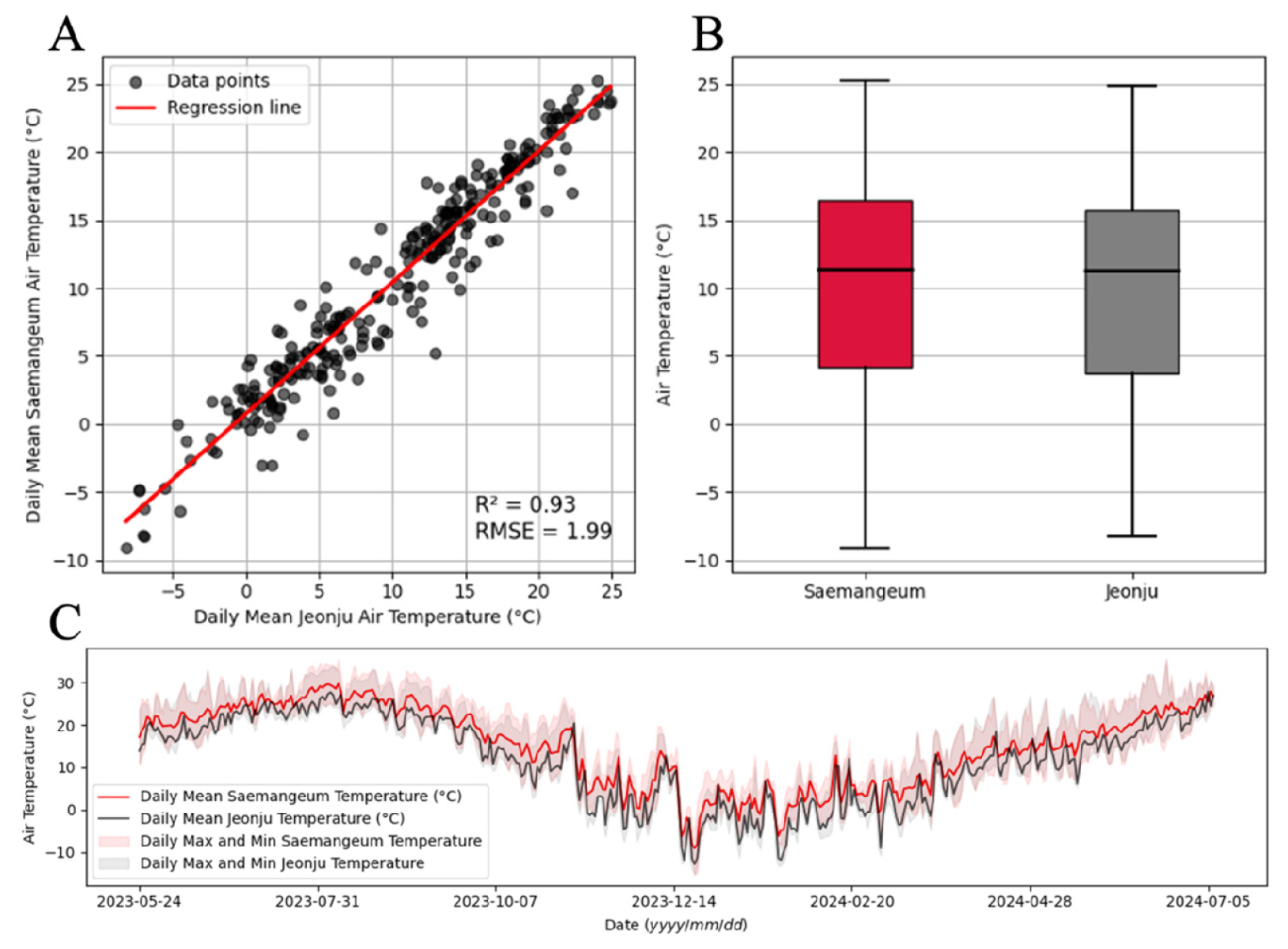
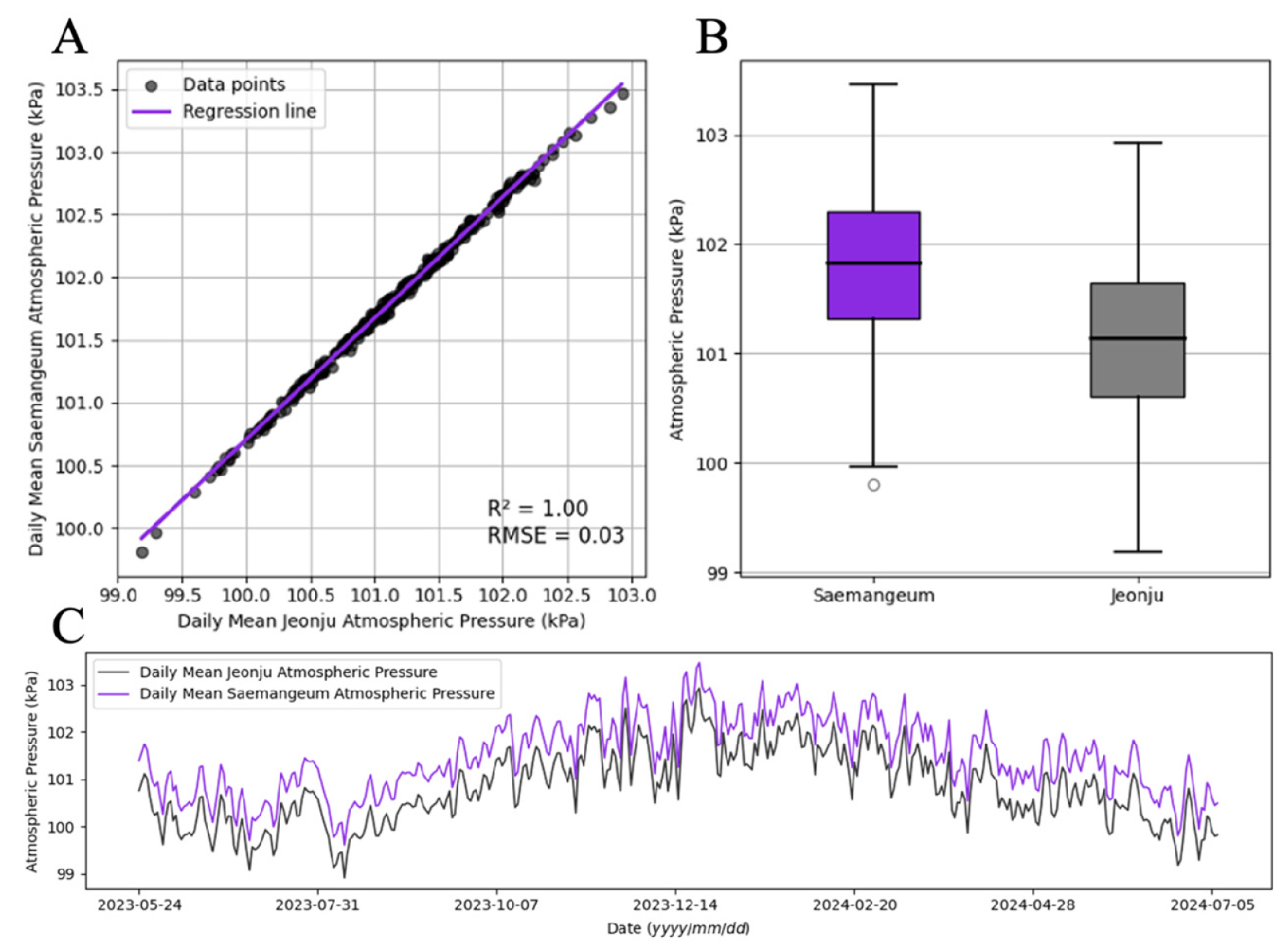
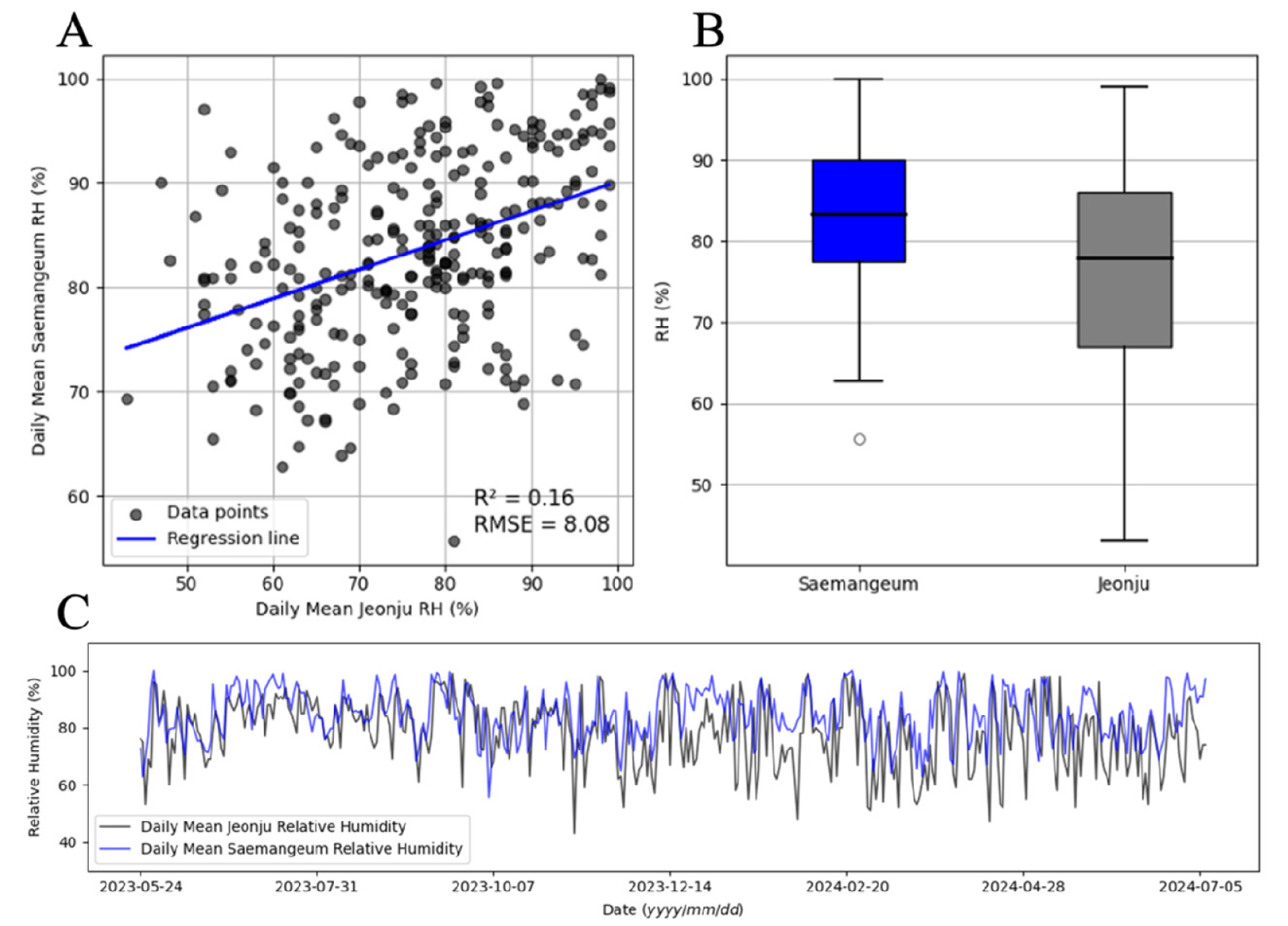
새만금 간척지와 내륙지역인 전주의 일사량, 온도의 R²값은 모두 0.93으로 매우 유사했으며(Figs. 2, 3) 기압은 R² = 1.00으로 상관관계가 강하지만 평균치는 약 0.7의 차이를 보였다. 모델에서 기후 데이터를 사용할 경우 기압이 모델에게 주는 영향이 미미하므로 기압을 해당 위치의 평균값으로 고정시키지만(Allen 등, 1998), 측정 결과 서로 다른 고도의 지역에서 기압의 경향은 같고 측정값의 차이를 확인할 수 있었다(Fig. 4). 습도는 R² = 0.16으로 상이하였으며, 평균은 약 5.9% 차이로 새만금이 더 높았다(Fig. 5). 마지막으로 풍속은 R² = 0.16으로 상관관계가 매우 약하였으며, 평균은 약 1m·s^-1 로 새만금이 내륙지역보다 크게 높았고 풍속의 범위도 새만금의 최솟값과 최댓값은 0.57m·s^-1과 7.80m·s^-1, 전주의 최솟값과 최댓값은 0.00m·s^-1와 4.50m·s^-1으로 새만금이 약 1.6배 넓었다(Fig. 6). 기준 증발산 모델의 값은 기후 데이터의 값에 의해 결정되기 때문에, 이처럼 기존의 내륙지역과 기후 특성이 다른 간척지 지역에 대한 모델의 성능 평가 및 사용의 필요성을 보여준다.

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F2.jpg

Fig. 2.

For daily average solar radiation in Saemangeum and Jeonju: Coefficient of determination (R²) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F3.jpg

Fig. 3.

For daily maximum, minimum, and average temperatures in Saemangeum and Jeonju: Coefficient of determination (R²) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F4.jpg

Fig. 4.

For daily average atmospheric pressure in Saemangeum and Jeonju: Coefficient of determination (R²) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F5.jpg

Fig. 5.

For daily average relative humidity in Saemangeum and Jeonju: Coefficient of determination (R²) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F6.jpg

Fig. 6.

For daily average wind speed in Saemangeum and Jeonju: Coefficient of determination (R²) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

2. 간척지 기준 증발산량 측정

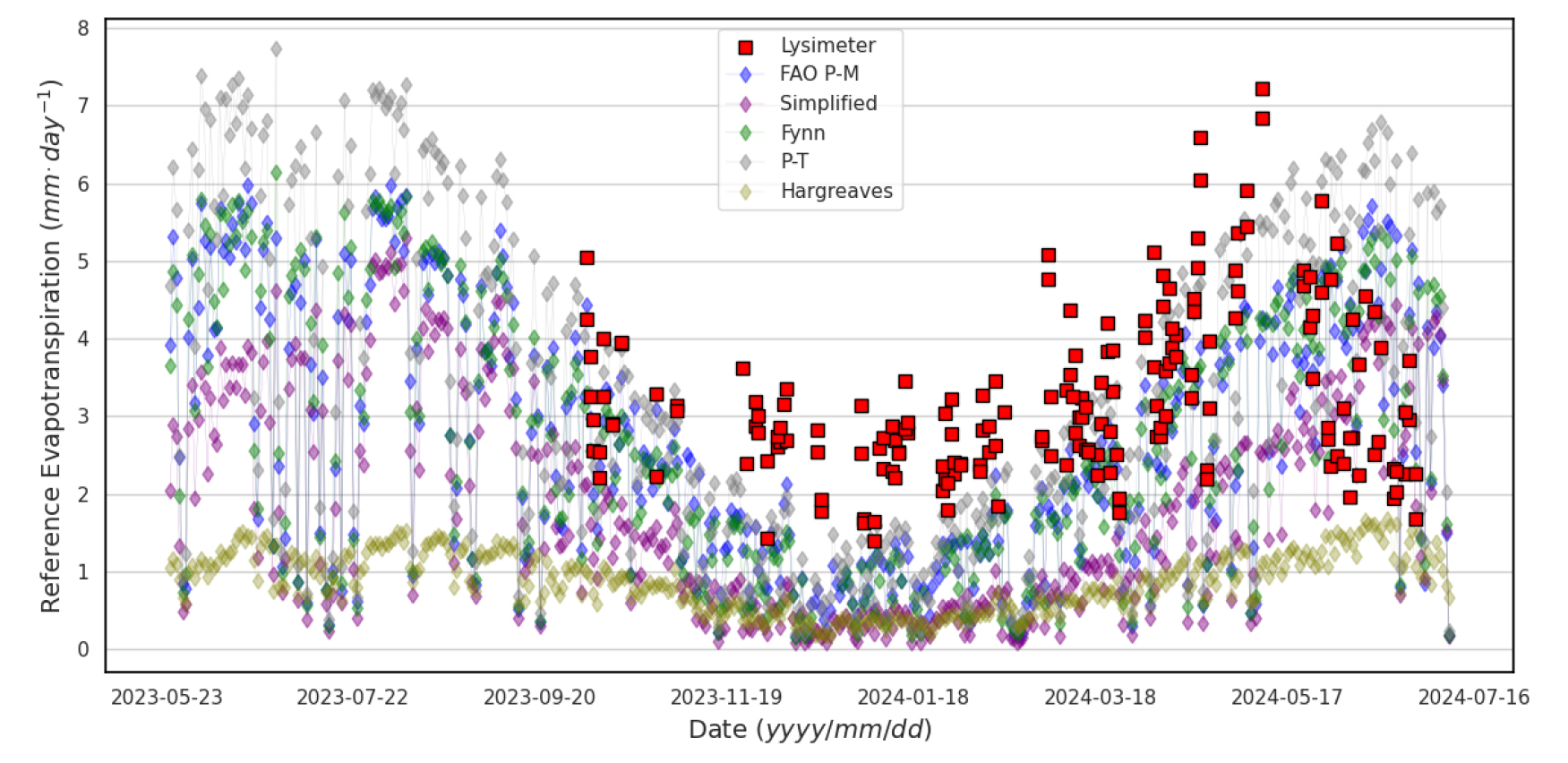
모델과 라이시미터 실측과 새만금 간척지 기후 데이터로 시뮬레이션 값은 Fig. 7과 같다. 라이시미터 실측 기준 증발산량은 겨울인 12, 1, 2월에 낮은 증발산량, 봄과 초여름인 4, 5, 6월에 높았다. 라이시미터 실측 기준 증발산량은 Table 3과 같이 일사량, 온도, 풍속과 양의 상관관계, 기압, 상대습도와는 음의 상관관계를 나타냈다.

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F7.jpg

Fig. 7.

Lysimeter measurements and values simulated with Saemangeum climate data for five reference evapotranspiration (ET_o) models: FAO Penman-Monteith equation (FAO P-M), Simplified equation (Simplified), Fynn equation (Fynn), Priestley-Taylor equation (P-T).

Table 3.

Correlation coefficient (R) and Coefficient of determination (R²) between lysimeter evapotranspiration and environmental factors at Saemangeum.

	Solar Radiation	Wind Speed	Air Temperature	Atomospheric Pressure	Relative Humidity
R	0.594	0.243	0.290	－0.274	－0.207
R²	0.353	0.059	0.084	0.075	0.043

식물은 증산을 통해 뿌리에서 물과 양분을 흡수하여 운반하고, 기공을 통해 수분이 증발하여 엽온을 낮춰 식물체 온도를 유지한다(Lambers 등, 2008; Nilson과 Assmann, 2007). 증산은 토양에서 물이 기화하여 발생하는 증발과 동시에 일어나기 때문에 분류하여 계산하기 어렵다(Allen 등, 1998; Schlesinger와 Jasechko, 2014). 두 개념을 합한 증발산량은 주로 토양 표면에 도달하는 태양 복사량에 의해 결정되기 때문에(Allen 등, 1998; Yin 등, 2008) Table 3과 같이 측정한 기준 증발산량이 일사량과 가장 높은 상관관계를 나타냈다. 또한 증발산으로 인해 습윤하고 따뜻해진 경계층을 높은 풍속이 불안정하게 하여(Wang 등, 2020) 잎 주변의 상대습도와 온도를 낮추어 증발산을 촉진시킨다(Allen 등, 1998; Stanghellini, 1987).

3. 간척지 기후에서의 적합한 기준 증발산 모델 성능 평가

모델 시뮬레이션 기준 증발산량도 라이시미터와 유사하였으며, 일사량과 비례하게 가을에 감소하여 겨울에는 낮고, 봄에 증가하여 여름에는 높은 경향을 보였다(Fig. 7). ‘2. 간척지 기준 증발산량 측정’에서 고찰한 증발산에 영향을 주는 환경 변수들이 시뮬레이션 한 5가지 모델에서도 반영되어 실측과 유사한 경향이 나타났다. 모델의 전체적인 시뮬레이션 값은 일사량 기반인 Priestley-Taylor 방정식이 가장 높고 에너지 밸런스 기반인 FAO Penman-Monteith 방정식, Fynn 방정식, Simplified 방정식과 온도 기반인 Hargreaves 방정식 순으로 높았다.

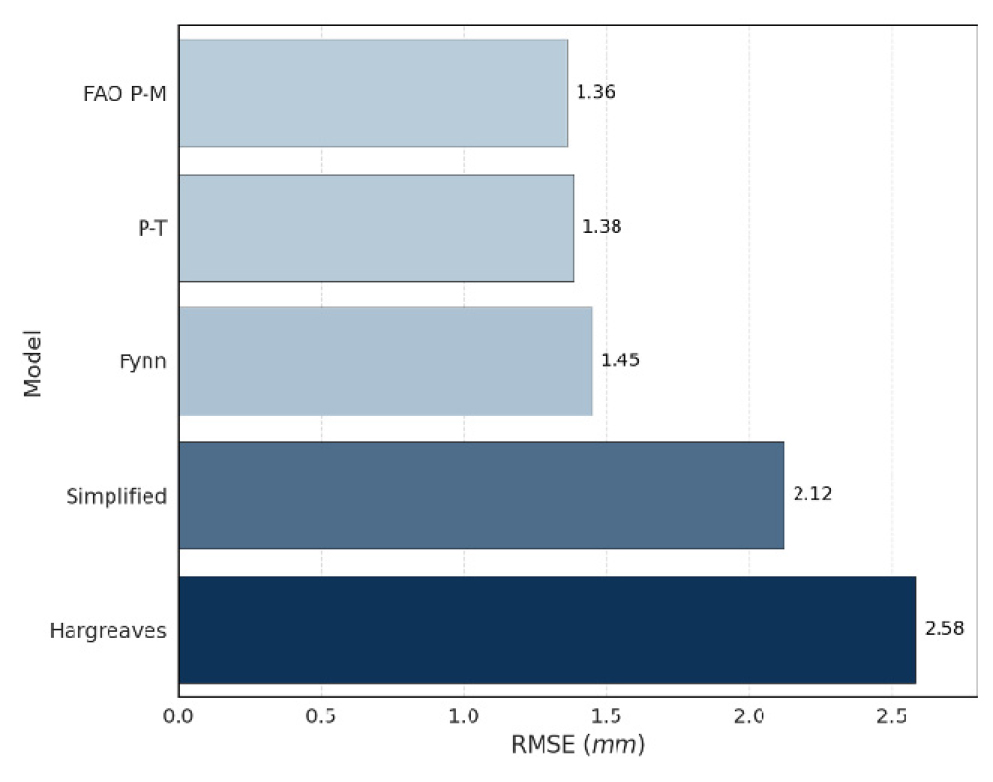
라이시미터 실측 증발산량과 비교한 5가지 모델의 평균 제곱근 편차(RMSE) 값은 FAO Penman-Monteith 방정식이 1.36, Priestley-Taylor 방정식이 1.38, Fynn 방정식이 1.45, Simplified 방정식이 2.12, Hargreaves 방정식이 2.58 순으로, 가장 높은 정확도를 보인 FAO Penman-Monteith 방정식과 두 번째로 높은 정확도를 보인 Priestley-Taylor 방정식과 비슷한 성능을 보였다(Fig. 8, Table 4). 이때 분산분석(ANOVA) 결과, Hargreaves 방정식을 제외한 4개 모델 간에 통계적으로 유의미한 차이가 확인되었다(F(3,392) = 23.533, p < 0.0001).

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F8.jpg

Fig. 8.

Root mean squared error RMSE for five reference evapotranspiration (ET_o) models based on a lysimeter: FAO Penman-Monteith equation (FAO P-M), Simplified equation (Simplified), Fynn equation (Fynn), Priestley-Taylor equation (P-T).

Table 4.

Root mean squared error (RMSE) for five reference evapotranspiration (ET_o) models based on a lysimeter.

ET_o Model

FAO Penman-Monteith

Simplified

Fynn

Priestley-Taylor

Hargreaves

FAO Penman-Monteith 방정식의 RMSE 값은 1.36으로, 라이시미터에서 실측한 일평균 ET_o 값이 3.2mm인 것을 고려할 때 다소 높은 오차율을 나타냈다. 이러한 결과는 모델들의 낮은 정확도를 나타내며, 높은 풍속과 습도 등 지역 특성에 적합한 모델 선정 및 연구의 필요성을 강조한다.

FAO Penman-Monteith 방정식은 고정된 표면 저항값을 사용하여 동적인 변화를 단순화하기에 넓은 범위의 풍속에서 부정확할 수 있다(Cai 등, 2007; Subedi와 Chávez, 2015). 그럼에도 불구하고 FAO Penman-Monteith 방정식이 가장 정확도가 높은 이유는 증발산량과 관련된 생물학적 및 물리적 과정을 통합하고 다양한 환경 변수를 종합적으로 고려하였기 때문이다(Allen 등, 1998). 특히, ET_o는 습한 지역에서 풍속의 영향이 낮은데(Koudahe 등, 2018), 이러한 환경 요소를 반영하여 방정식에서 풍속(u₂) 항과 수증기압포차(e_s-e_a) 항을 조합하고, 이로 인해 높은 상대습도 조건에서 풍속이 높아도 안정적으로 증발산 값을 도출하기 때문이다. FAO Penman-Monteith 방정식과 비슷한 성능인 Priestley-Taylor 방정식이 두 번째로 정확도가 높은 이유는 모델이 습한 표면에서 증발을 더 정확하게 추정하며(Eichinger 등, 1996) Table 5와 같이 방정식에 간척지의 넓은 범위의 풍속과 높은 습도를 반영하는 항이 없기 때문이다. Fynn 방정식과 Simplified 방정식은 같은 환경 변수인 일사량, 온도, 상대습도를 공유한다(Table 5). 그럼에도 불구하고 두 모델이 성능 차이를 나타내는 이유는 Simplified 방정식이 포화 수증기압에 대해 광범위하게 반응하고(Baille 등, 1994) Fynn 방정식은 증발산량이 주로 일사량의 영향을 받는다는 것을 고려하여 개발되었기 때문으로(Fynn 등, 1993) 판단된다.

Table 5.

Required meteorological data for using each reference evapotranspiration (ET_o) model : Rn (Net Radiation), u (Wind Speed), T_a (air Temperature), RH (Relative Humidity), P (Air Pressure).

ET_o Model	R_n	u	T_a	RH	P (Replaceable with a constant 101.3 kPa)
FAO Penman - Monteith	o	o	o	o	o
Simplified	o		o	o	o
Fynn	o		o	o	o
Priestley-Taylor	o		o		o
Hargreaves			o

풍속과 습도의 영향을 받지 않는 Hargreaves 방정식은 Priestley-Taylor와 달리 가장 낮은 정확성을 보였는데, 이는 연중 일수와 위도로 계산되는 대기 외 일사량이 빈번한 해무와 같은 실제 새만금의 기후 특성을 반영하지 못하기 때문이다(Gao 등, 2007; Lee 등, 2014). 또한 2024년 3월 13일과 20일에 온도는 0.12°C 차이로 전체범위의 0.3%, 0.2%로 유사한 값을 보였고, 풍속은 3.09m·s^-1, 습도는 17.9% 차이로 각각 전체범위의 42.7%, 40.4%로 큰 차이를 보였다(Figs. 2,3,4,5,6). 이때 라이시미터 실측 값은 1.16mm·day^-1 차이로 전체범위의 21.1%인 반면, Hargreaves 방정식 추정 값은 0.06mm·day^-1차이로 전체범위의 3.7%로 상대적으로 낮은 차이를 나타냈다(Fig. 7). 이는 실제 기준 증발산에 풍속과 습도가 영향을 미치지만, Hargreaves 방정식은 풍속과 습도를 반영하지 않기 때문이다. 이처럼 Table 4의 RMSE 값과 Table 5에서의 환경 변수 항목을 통해 모델에 사용되는 환경 변수가 모델의 정확도에 영향을 주는 것을 확인할 수 있다.

새만금 기후에서 5가지 기준 증발산 모델을 시뮬레이션 하여 라이시미터 실측 기준 증발산량과 비교한 결과, 높은 성능을 보였던 FAO Penman-Monteith 방정식과 Priestley-Taylor 방정식이 풍속의 범위가 넓고 높으며 상대습도가 높은 간척지 지역에서 사용하기 적합한 기준 증발산 모델이라 판단된다.

간척지 기준 증발산 예측은 FAO Penman-Monteith 방정식이 가장 정확하지만, 일사량, 온도, 풍속, 상대습도 등 많은 환경 변수 측정을 요구한다(Table 5)(Cai 등, 2007). 반면 Priestley-Taylor 방정식은 FAO Penman-Monteith 방정식과 비슷한 성능이며 일사량과 온도만으로 기준 증발산 예측이 가능하기 때문에 상대습도와 풍속 데이터 수집이 어려운 경우에도 FAO Penman-Monteith 방정식의 정확도 만큼 기준 증발산량을 계산할 수 있을 것으로 판단된다.

4. 간척지와 내륙지역 기준 증발산량 비교

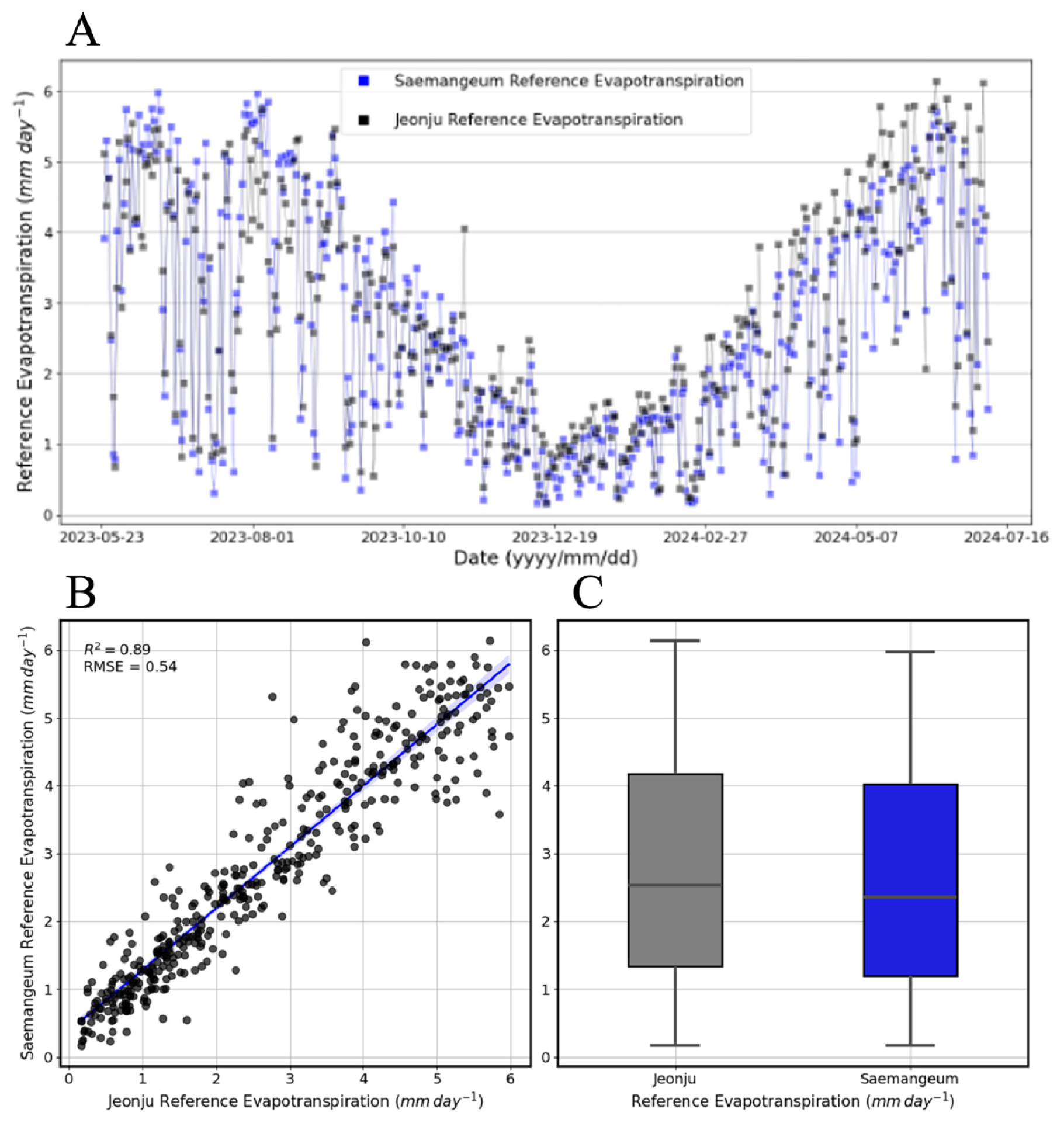
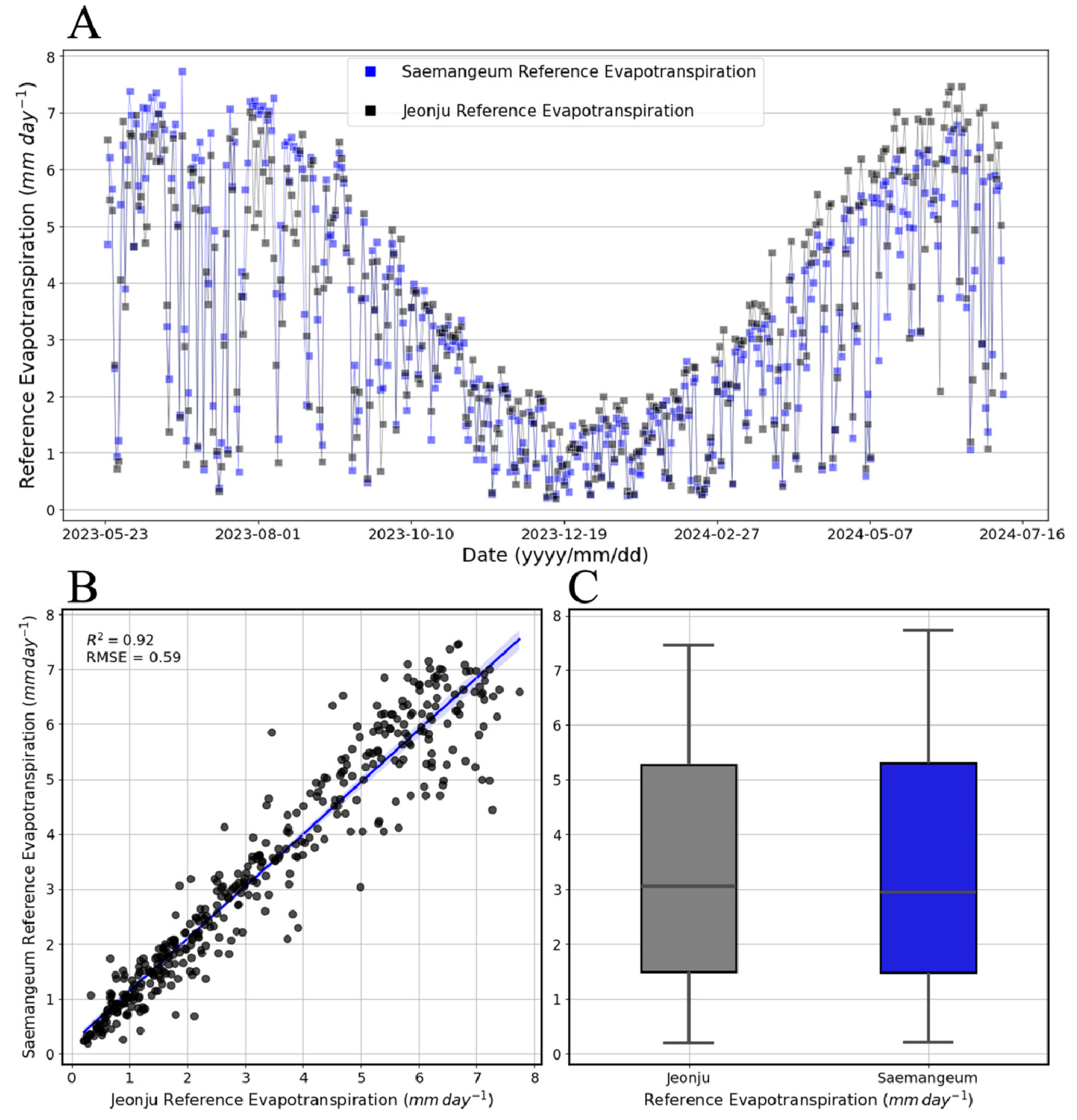
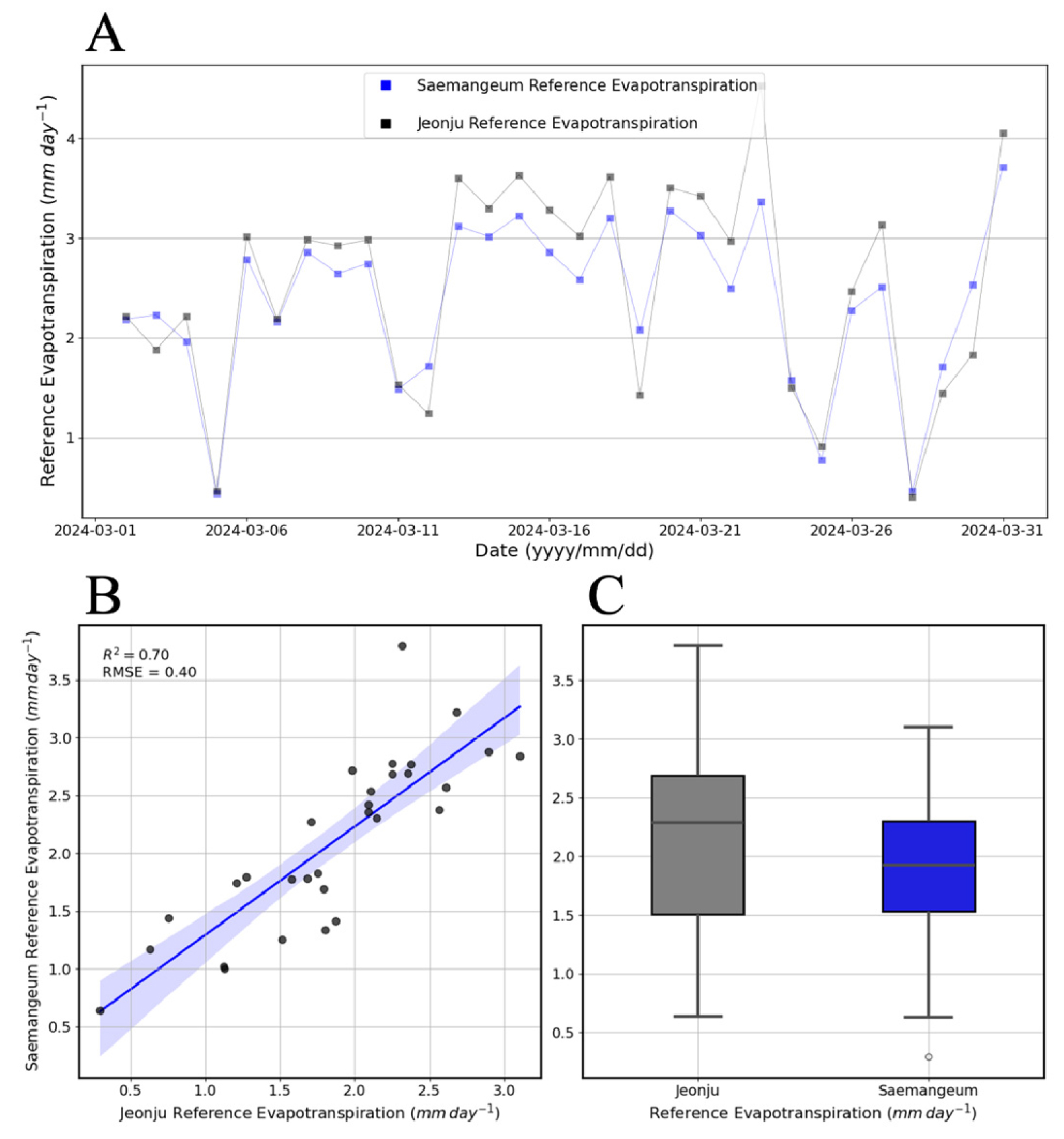
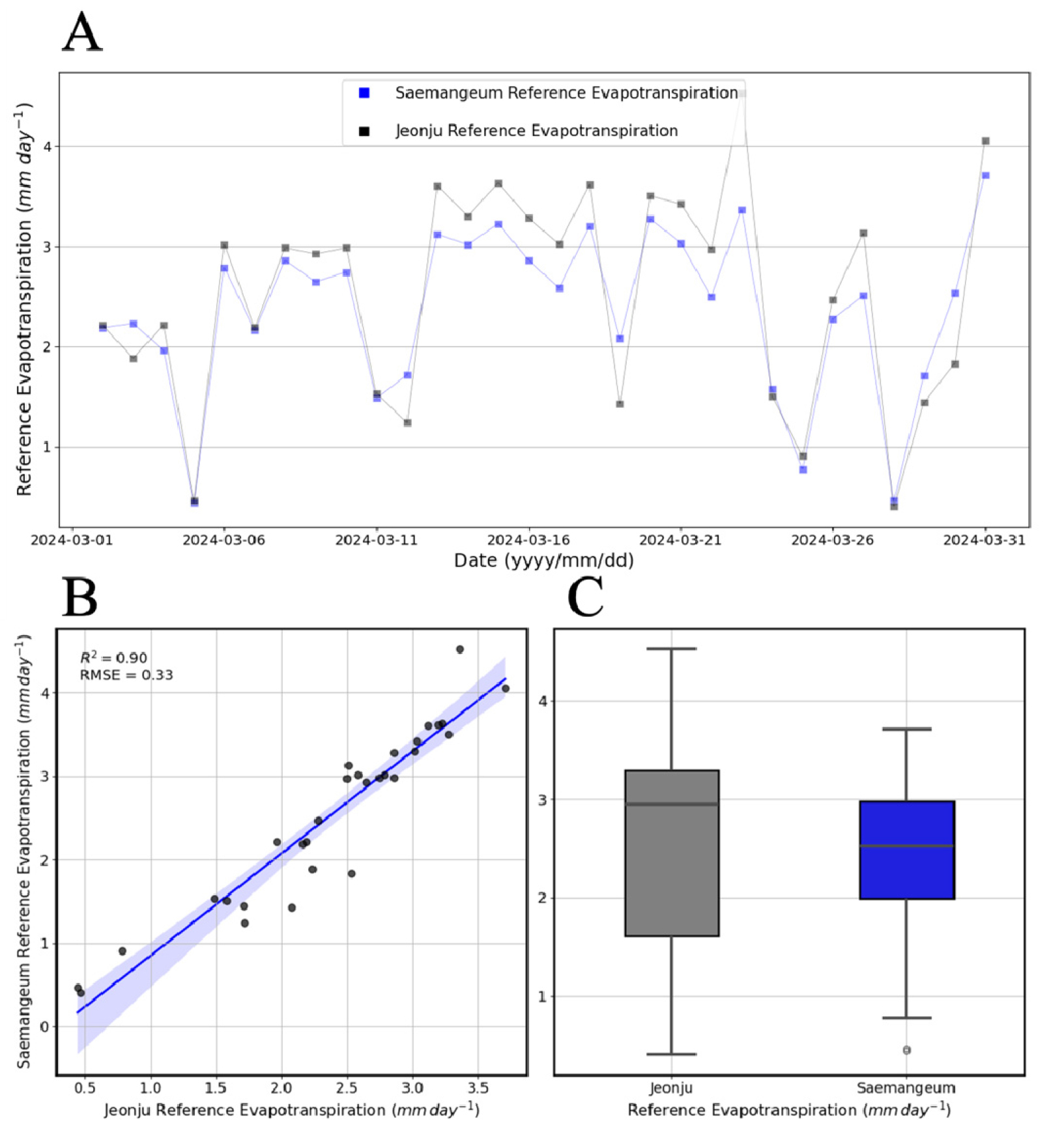
새만금 간척지 기후에서 가장 높은 성능을 보인 FAO Penman-Monteith 방정식, Priestley-Taylor 방정식을 같은 기간 내륙지역인 전주시에 적용하고 비교하였다. 두 지역 간의 증발산량 유사도는 FAO Penman-Monteith 방정식에서 R² = 0.89, RMSE = 0.54(Fig. 9), Priestley-Taylor 방정식에서 R² = 0.92, RMSE = 0.59(Fig. 10)이다. 분석 기간에는 두 지역에서 기존 증발산량이 두 모델이 비슷하나, 두 지역의 풍속이 가장 상이한 초봄인 2024년 3월 2일부터 2024년 3월 31일까지의 기간에 두 지역의 ET_o를 비교하였을 때, Priestley-Taylor 방정식은 R² = 0.70, RMSE = 0.40(Fig. 11), FAO Penman-Monteith 방정식은 R² = 0.90, RMSE = 0.33(Fig. 12)으로 나타났다. FAO Penman-Monteith 방정식은 Priestley-Taylor 방정식과 다르게 풍속의 영향을 받아 두 지역간의 ET_o가 낮은 유사도를 나타냈다. 따라서 간척지의 풍속이 넓고 높다는 점을 고려할 때, 풍속을 반영하며 가장 정확한 성능을 보인 FAO Penman-Monteith 방정식을 사용하는 것이 가장 적절한 것으로 판단된다.

새만금의 기후는 내륙과 상이한 기후 조건을 보였으며, 기존의 모델로 산출된 증발산량이 정확하지 않았음을 보였다. 특히 기존에 널리 사용되며 풍속과 상대습도의 영향을 모두 받는 FAO Penman-Monteith 방정식이 5가지 모델 중 가장 높은 정확도를 보였으나, 라이시미터 실측 값에 대해 낮은 정확성을 확인하였다. 따라서 본 연구는 간척지와 같은 특수한 환경뿐만 아니라 각 기후 및 환경 특성에 따라 적합한 모델 사용의 중요성을 나타내며, 추후 다양한 재배 환경에 대한 증발산량 산정 연구가 진행되어야 할 것으로 판단된다.

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F9.jpg

Fig. 9.

Reference evapotranspiration (ET_o) (A), Regression analysis (B), and range and mean (C) for Saemangeum and Junju estimated using FAO penman-Monteith equation.

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F10.jpg

Fig. 10.

Reference evapotranspiration (ET_o) (A), Regression analysis (B), and range and mean (C) for Saemangeum and Junju estimated using Priestley-Taylor equation.

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F11.jpg

Fig. 11.

Reference evapotranspiration (ET_o) (A), Regression analysis (B), and range and mean (C) for early spring in Saemangeum and Junju estimated using FAO Penman-Monteith equation.

https://cdn.apub.kr/journalsite/sites/phpf/2024-033-04/N0090330420/images/phpf_2024_334_373_F12.jpg

Fig. 12.

Reference evapotranspiration (ET_o) (A), Regression analysis (B), and range and mean (C) for early spring in Saemangeum and Junju estimated using Priestley-Taylor equation.

Acknowledgements

본 연구는 농촌진흥청 공동연구사업(과제번호:RS-2023-00231192)의 지원에 의해 이루어진 것임.

References

Abbady F.A., A. Abdelgalil, A.A. Mustafa, and M.R.M. Ahmed 2021, Response of two wheat varieties to salt stress of newly reclaimed soil in Upper Egypt. Journal of Soil Sciences and Agricultural Engineering 12:757-762. doi:10.21608/jssae.2021.207251

10.21608/jssae.2021.207251

Allen R.G., L.S. Pereira, D. Raes, and M. Smith 1998, Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO, Rome 300:D05109.

Bae H.S., J.B. Hwang, H.S. Kim, B.I. Koo, I.B. Choi, T.S. Park, H.K. Park, S.H. Lee, Y.Y. Lee, S.H. Lee, and G.H. Lee 2015, Effects of drip irrigation on soil salinity and growth of green cauliflower in the reclaimed land of Saemangeum. Protected Horticulture and Plant Factory 24:275-280. doi:10.12791/KSBEC.2015.24.4.275

10.12791/KSBEC.2015.24.4.275

Baille M., A. Baille, and J.C. Laury 1994, A simplified model for predicting evapotranspiration rate of nine ornamental species vs. climate factors and leaf area. Sci Hortic 59:217-232. doi:10.1016/0304-4238(94)90015-9

10.1016/0304-4238(94)90015-9

Cai J., Y. Liu, T. Lei, and L.S. Pereira 2007, Estimating reference evapotranspiration with the FAO Penman-Monteith equation using daily weather forecast messages. Agric For Meteorol 145:22-35. doi:10.1016/j.agrformet.2007.04.012

10.1016/j.agrformet.2007.04.012

Eichinger W.E., M.B. Parlange, and H. Stricker 1996, On the concept of equilibrium evaporation and the value of the Priestley‐Taylor coefficient. Water Resour Res 32:161-164. doi:10.1029/95WR02920

10.1029/95WR02920

Fazlil-Ilahil W.F. 2009, Evapotranspiration models in greenhouse. MSc, Wageningen agricultural University, Wageningen, Netherlands.

Food and Agriculture Organization (FAO) 2024, Agriculture water management. Food and Agriculture Organization.

Fynn R.P., A. Al-Shooshan, T.H. Short, and R.W. McMahon 1993, Evapotranspiration measurement and modeling for a potted chrysanthemum crop. Transactions of the ASAE 36:1907-1913. doi:10.13031/2013.28541

10.13031/2013.28541

Gao S., H. Lin, B. Shen, and G. Fu 2007, A heavy sea fog event over the Yellow Sea in March 2005: Analysis and numerical modeling. Adv Atmos Sci 24:65-81. doi:10.1007/s00376-007-0065-2

10.1007/s00376-007-0065-2

Hah J., and I.B. Lee 2014, Presentation 2: Field of biological production facilities and environmental engineering; 12:24-12:36: Validation of CFD models through PIV experiments in a wind tunnel and analysis of ventilation rates in a reclaimed land greenhouse with natural ventilation. J Korean Soc Manuf Technol Eng 19:49-51. (in Korean)

Hargreaves G.H., and Z.A. Samani 1985, Reference crop evapotranspiration from temperature. Appl Eng Agric 1:96-99. doi:10.13031/2013.26773

10.13031/2013.26773

Jeong Y.J., S.S. Lim, H.J. Park, B.S. Seo, S.I. Park, J.H. Ryu, K.S. Lee, D.Y. Chung, H.Y. Kim, S.H. Lee, H.I. Yang, and W.J. Choi 2020, Evaluation of crop suitability for reclaimed tideland soils using soil and water salinity and soil texture. Korean J Soil Sci Fert 53:70-81. doi:10.7745/KJSSF.2020.53.1.070

10.7745/KJSSF.2020.53.1.070

Kang S.I., S. Eom, S.Y. Yoo, S. Kang, and T.W. Kim 2023, Assessment of drought stress in maize growing in coastal reclaimed lands on the Korean Peninsula using vegetation index. Korean J Environ Biol 41:283-290. doi:10.11626/KJEB.2023.41.3.283

10.11626/KJEB.2023.41.3.283

Kashyap P.S., and R.K. Panda 2001, Evaluation of evapotranspiration estimation methods and development of crop-coefficients for potato crop in a sub-humid region. Agric Water Manag 50:9-25. doi:10.1016/S0378-3774(01)00102-0

10.1016/S0378-3774(01)00102-0

Katsoulas N., and C. Stanghellini 2019, Modelling crop transpiration in greenhouses: Different models for different applications. Agronomy 9:392. doi:10.3390/agronomy9070392

10.3390/agronomy9070392

Kim H.J., G.R. Kim, H.N. Woo, S.H. Park, J.H. Shin, Y.C. Choi, and D.Y. Chung 2011, Properties and fate of nitrogen in a reclaimed tidal soil. Korean J Agric Sci 38:301-307.

Kim H.S., K.R. Kim, J.E. Yang, Y.S. Ok, G. Owens, T. Nehls, G. Wessolek, and K.H. Kim 2016, Effect of biochar on reclaimed tidal land soil properties and maize (Zea mays L.) response. Chemosphere 142:22-31. doi:10.1016/j.chemosphere.2015.06.041

10.1016/j.chemosphere.2015.06.04126138709

Korea Development Institute (KDI) 2023 Reassessment Report on the Feasibility of Business Plan: Saemangeum District (Internal Development) Comprehensive Reclamation Development Project. (in Korean)

Koudahe K., K. Djaman, and J.K. Adewumi 2018, Evaluation of the Penman-Monteith reference evapotranspiration under limited data and its sensitivity to key climatic variables under humid and semiarid conditions. Model Earth Syst Environ 4:1239-1257. doi:10.1007/s40808-018-0497-y

10.1007/s40808-018-0497-y

Lambers H., F.S. Chapin, and T.L. Pons 2008, Plant Physiological Ecology, Vol. 2, No. 1, Springer, New York, USA, pp 11-99. doi:10.1007/978-0-387-78341-3_2

10.1007/978-0-387-78341-3_2

Lee I.B., D.H. Jung, P.H. Yi, J.G. Lee, and S.R. Bhandari 2021, Changes in growth, nutrient uptake, and glucosinolate content of Chinese cabbage grown in reclaimed land under different irrigation salinity levels. (in Korean)

Lee J.W., J.H. Shin, J.H. Kim, H.W. Park, I.H. Yoo, and J.Y. Son 2014, Analysis of light environment characteristics in reclaimed land and prediction of spatial light distribution in greenhouses using a 3-D model. Journal of Facility Horticulture and Plant Factory 23:303-308. doi:10.12791/KSBEC.2014.23.4.303

10.12791/KSBEC.2014.23.4.303

Liu H.J., S. Cohen, J. Tanny, J.H. Lemcoff, and G. Huang 2008, Estimation of banana (Musa sp.) plant transpiration using a standard 20 cm pan in a greenhouse. Irrig Drain 22:311-323.

10.1007/s10795-008-9058-2

Liu X., C. Xu, X. Zhong, Y. Li, X. Yuan, and J. Cao 2017, Comparison of 16 models for reference crop evapotranspiration against weighing lysimeter measurement. Agric Water Manage 184:145-155. doi:10.1016/j.agwat.2017.01.017

10.1016/j.agwat.2017.01.017

Nam S.W., and H.H. Shin 2017, Analysis of ventilation and cooling characteristics in a reclaimed land greenhouse. Facility Horticulture and Plant Factory 26:181-187. doi:10.12791/KSBEC.2017.26.3.181

10.12791/KSBEC.2017.26.3.181

Nilson S.E., and S.M. Assmann 2007, The control of transpiration. Insights from Arabidopsis. Plant Physiology 143:19-27. doi:10.1104/pp.106.093161

10.1104/pp.106.09316117210910PMC1761994

Oh Y.Y., S.Y. Yoo, H.K. Ock, S.H. Lee, H.S. Lee, K.S. Lee, ... and T.W. Kim 2022, Growth characteristics of maize under different salinity levels and drought stress periods in the reclaimed land of Saemangeum. In Proceedings of the Korean Society of Crop Science Conference, pp 87-87. (in Korean)

Oke T.R. 2002, Boundary Layer Climates. Routledge, London, UK. doi:10.4324/9780203407219

10.4324/9780203407219PMC3166529

Prenger J.J., R.P. Fynn, and R.C. Hansen 2002, A comparison of four evapotranspiration models in a greenhouse environment. Transactions of the ASAE 45:1779-1785. doi:10.13031/2013.11429

10.13031/2013.11429

Priestley C.H.B., and R.J. Taylor 1972, On the assessment of surface heat flux and evaporation using large-scale parameters. Mon Weather Rev 100:81-92. doi:10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2

10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2

Ryu J.H., Y.Y. Oh, S.H. Lee, Y.J. Kim, J.T. Lee, J.W. Jeong, J.G. Jeon, S. Kim, and J.M. Lee 2020, Development of soil and water management techniques to mitigate re-salinization damage in reclaimed farmlands (Final Report). National Institute of Crop Science, Rural Development Administration.

Schlesinger W.H., and S. Jasechko 2014, Transpiration in the global water cycle. Agric For Meteorol 189:115-117. doi:10.1016/j.agrformet.2014.01.011

10.1016/j.agrformet.2014.01.011

Stanghellini C. 1987, Transpiration of greenhouse crops: an aid to climate management. Wageningen University and Research, Gelderland, Nederlands.

Subedi A., and J.L. Chávez 2015, Crop evapotranspiration (ET) estimation models: a review and discussion of the applicability and limitations of ET methods. J Agric Sci 7:50. doi:10.5539/jas.v7n6p50

10.5539/jas.v7n6p50

Wang S., Q. Zhang, P. Yue, and J. Wang 2020, Effects of evapotranspiration and precipitation on dryness/wetness changes in China. Theor Appl Climatol 142:1027-1038. doi:10.1007/s00704-020-03336-8

10.1007/s00704-020-03336-8

Yin Y., S. Wu, D. Zheng, and Q. Yang 2008, Radiation calibration of FAO56 Penman-Monteith model to estimate reference crop evapotranspiration in China. Agric Water Manage 95:77-84. doi:10.1016/j.agwat.2007.09.002

10.1016/j.agwat.2007.09.002

Zhao Y., Y. Chen, C. Wu, G. Li, M. Ma, L. Fan, H. Zheng, L. Song, and X. Tang 2023, Exploring the contribution of environmental factors to evapotranspiration dynamics in the Three-River-Source region, China. J Hydrol 626:130222. doi:10.1016/j.jhydrol.2023.130222

10.1016/j.jhydrol.2023.130222

Journal of Bio-Environment Control ISSN:1229-4675(Print) 2765-3641(Online) 생물환경조절학회지

Preview

Performance Evaluation of a Reference Evapotranspiration Model in Reclaimed Land Environments and Comparison with Inland Areas

ABSTRACT

MAIN

Fig. 1.

Weather sensor ATMOS 41W (Meter Group Inc., Pullman, WA, USA) (A) and lysimeter (BWL-LY500, Hanul, Daejeon, South Korea) (B) installed in Saemangeum.

Table 1.

Five Reference Evapotranspiration (ETo) models used for predicting evapotranspiration in Saemangeum.

Table 2.

Definition and units of parameters used in each evapotranspiration model.

Fig. 2.

For daily average solar radiation in Saemangeum and Jeonju: Coefficient of determination (R2) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

Fig. 3.

For daily maximum, minimum, and average temperatures in Saemangeum and Jeonju: Coefficient of determination (R2) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

Fig. 4.

For daily average atmospheric pressure in Saemangeum and Jeonju: Coefficient of determination (R2) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

Fig. 5.

For daily average relative humidity in Saemangeum and Jeonju: Coefficient of determination (R2) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

Fig. 6.

For daily average wind speed in Saemangeum and Jeonju: Coefficient of determination (R2) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

Fig. 7.

Lysimeter measurements and values simulated with Saemangeum climate data for five reference evapotranspiration (ETo) models: FAO Penman-Monteith equation (FAO P-M), Simplified equation (Simplified), Fynn equation (Fynn), Priestley-Taylor equation (P-T).

Table 3.

Correlation coefficient (R) and Coefficient of determination (R2) between lysimeter evapotranspiration and environmental factors at Saemangeum.

Fig. 8.

Root mean squared error RMSE for five reference evapotranspiration (ETo) models based on a lysimeter: FAO Penman-Monteith equation (FAO P-M), Simplified equation (Simplified), Fynn equation (Fynn), Priestley-Taylor equation (P-T).

Table 4.

Root mean squared error (RMSE) for five reference evapotranspiration (ETo) models based on a lysimeter.

Table 5.

Required meteorological data for using each reference evapotranspiration (ETo) model : Rn (Net Radiation), u (Wind Speed), Ta (air Temperature), RH (Relative Humidity), P (Air Pressure).

Fig. 9.

Reference evapotranspiration (ETo) (A), Regression analysis (B), and range and mean (C) for Saemangeum and Junju estimated using FAO penman-Monteith equation.

Fig. 10.

Reference evapotranspiration (ETo) (A), Regression analysis (B), and range and mean (C) for Saemangeum and Junju estimated using Priestley-Taylor equation.

Fig. 11.

Reference evapotranspiration (ETo) (A), Regression analysis (B), and range and mean (C) for early spring in Saemangeum and Junju estimated using FAO Penman-Monteith equation.

Fig. 12.

Reference evapotranspiration (ETo) (A), Regression analysis (B), and range and mean (C) for early spring in Saemangeum and Junju estimated using Priestley-Taylor equation.

Acknowledgements

References

Five Reference Evapotranspiration (ET_o) models used for predicting evapotranspiration in Saemangeum.

For daily average solar radiation in Saemangeum and Jeonju: Coefficient of determination (R²) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

For daily maximum, minimum, and average temperatures in Saemangeum and Jeonju: Coefficient of determination (R²) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

For daily average atmospheric pressure in Saemangeum and Jeonju: Coefficient of determination (R²) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

For daily average relative humidity in Saemangeum and Jeonju: Coefficient of determination (R²) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

For daily average wind speed in Saemangeum and Jeonju: Coefficient of determination (R²) and root mean squared error (RMSE) (A), mean and range (B), time series graph (C).

Lysimeter measurements and values simulated with Saemangeum climate data for five reference evapotranspiration (ET_o) models: FAO Penman-Monteith equation (FAO P-M), Simplified equation (Simplified), Fynn equation (Fynn), Priestley-Taylor equation (P-T).

Correlation coefficient (R) and Coefficient of determination (R²) between lysimeter evapotranspiration and environmental factors at Saemangeum.

Root mean squared error RMSE for five reference evapotranspiration (ET_o) models based on a lysimeter: FAO Penman-Monteith equation (FAO P-M), Simplified equation (Simplified), Fynn equation (Fynn), Priestley-Taylor equation (P-T).

Root mean squared error (RMSE) for five reference evapotranspiration (ET_o) models based on a lysimeter.

Required meteorological data for using each reference evapotranspiration (ET_o) model : Rn (Net Radiation), u (Wind Speed), T_a (air Temperature), RH (Relative Humidity), P (Air Pressure).

Reference evapotranspiration (ET_o) (A), Regression analysis (B), and range and mean (C) for Saemangeum and Junju estimated using FAO penman-Monteith equation.

Reference evapotranspiration (ET_o) (A), Regression analysis (B), and range and mean (C) for Saemangeum and Junju estimated using Priestley-Taylor equation.

Reference evapotranspiration (ET_o) (A), Regression analysis (B), and range and mean (C) for early spring in Saemangeum and Junju estimated using FAO Penman-Monteith equation.

Reference evapotranspiration (ET_o) (A), Regression analysis (B), and range and mean (C) for early spring in Saemangeum and Junju estimated using Priestley-Taylor equation.