서 론
재료 및 방법
1. 재배 조건
2. 데이터 수집 및 전처리
3. 생체중 회귀식
4. 합성곱 신경망
결과 및 고찰
1. 생체중 회귀 결과
2. 합성곱 신경망 정확도
3. 생체중 추정 결과 분석
4. 한계 및 발전 방향
서 론
온실은 재배 환경을 능동적으로 제어하여 작물에 대한 계절의 영향을 줄이고 작물 생장을 돕는 역할을 한다. 능동 환경 제어에는 에너지가 필요하기 때문에 작물 생장이 적절하게 유지되어야 충분한 경제성을 달성할 수 있다(Dadhwal, 2003; South 등, 2019). 작물 생장에 있어서 생체중은 전체적인 작물의 상태를 가늠할 수 있는 주요 생육 지표이다(Berman과 DeJong, 1996; Huang 등, 2017). 따라서, 작물의 생체중을 추정할 수 있다면 작물 재배에 있어서 효율적으로 작물 환경을 조성할 수 있다.
작물의 생체중을 추정 및 측정하기 위해 다양한 연구가 시도되었고, 주로 회귀 분석과 모델링을 이용하는 연구가 있었다(Cho 등, 2007; Mokhtarpour 등, 2010). 이러한 경우 회귀식과 모델식을 적절히 설정해야 해당 모델이 적합한 설명력을 가질 수 있고, 파라미터 최적화를 위해 많은 생육 데이터를 수집해야 한다는 단점이 있다. 로드셀을 이용하여 생체중을 직접 측정하기도 하였다(Lee와 Son, 2019). 직접 측정은 생체중을 그대로 측정하는 방법으로 가장 정확하게 측정할 수 있는 가능성이 있으나, 작물의 무게를 측정할 수 있는 측정 장치를 설치하여야 하며, 복잡한 작물 환경 내 수분 흐름을 고려하여야 한다.
최근에 딥러닝, 특히 합성곱 신경망(Convolution neural network)을 사용한 이미지 처리 연구가 증가하고 있다(McCann 등, 2017Rawat과 Wang, 2017; Anwar 등, 2018). 합성곱 신경망은 미가공 데이터 상태의 이미지를 이용하여 신경망의 필터 구조로 이미지의 특징을 자동으로 추출할 수 있다. 이때, 미가공 데이터 상태의 이미지만을 활용하여 추론을 통해 추상적인 결과를 도출할 때 기존 모델들에 비해 더 높은 정확도를 보여주고 있다. 이미지는 그 자체만으로도 많은 정보를 담고 있기 때문에 이미지 처리는 다양한 가능성을 보여주고 있다. 특히, 자동화된 특징 추출로 인해 합성곱 신경망을 이용하면 기존에 요구되었던 복잡한 데이터 전처리나 모델 탐색 없이 미가공 데이터를 사용하여 쉽게 특정 업무를 처리하는 모델을 만들 수 있다.
작물의 이미지를 이용하여 간단한 이미지 처리 후 엽면적을 추정하는 연구도 시도되었다(Abràmoff 등, 2004). 작물의 미가공 데이터 이미지와 합성곱 신경망을 활용한 연구들도 또한 최근 많이 진행되었으나 대부분 질병과 관련된 경우가 많았으며(Shen 등, 2017; Picon 등, 2019; ), 미가공 데이터의 이미지를 이용하여 생체중을 추정한 예는 없었다.
본 연구의 목적은 합성곱 신경망을 이용하여 미가공 데이터 상태인 특정 시점의 파프리카 이미지를 입력으로 작물의 생체중을 추정하는 것이다.
재료 및 방법
1. 재배 조건
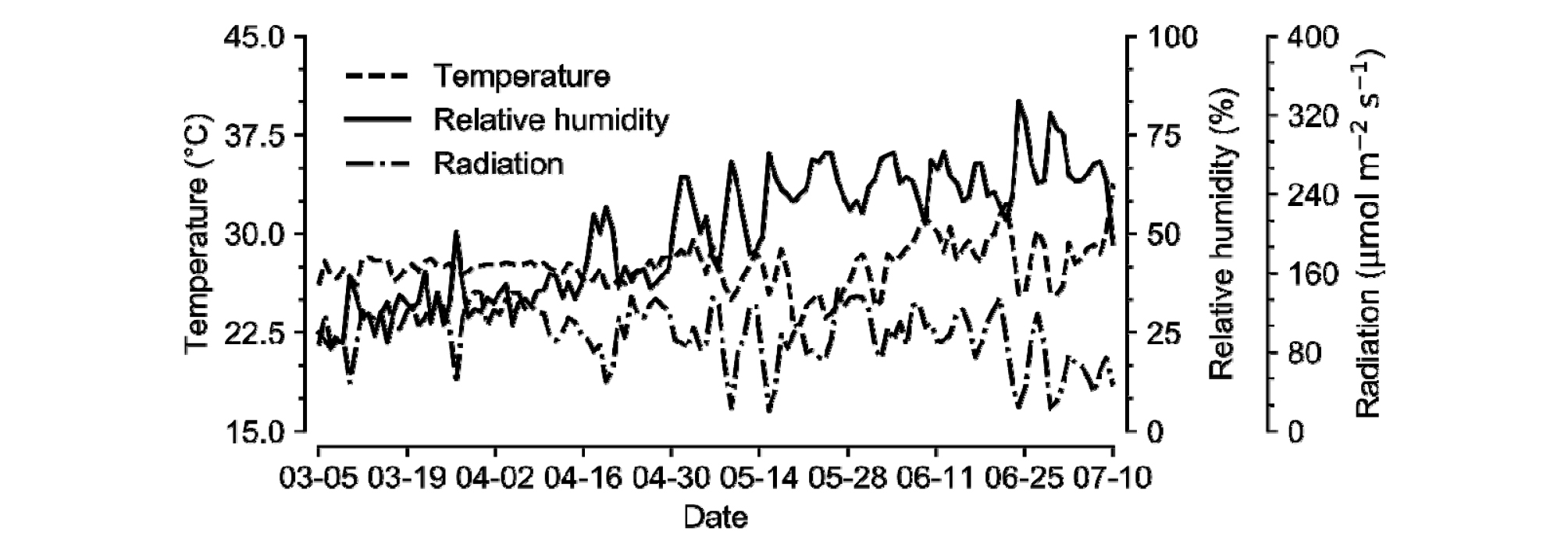
실험은 경기도 수원시(37.3°N 127.0°E)에 위치한 서울대학교 실험 온실에서 수행하였고, 파프리카(Capsicum annuum L. cv. Kori)를 사용하였다 (Fig. 1). 온실은 벤로형 온실이었으며, 측창과 천창은 온도가 26℃ 이상일 때 열리게 설정하였다. 파프리카는 2020년 2월 26일에 암면 블록과 암면 슬라브에 올려 정식하였다. 재식밀도는 m2 당 3.3개체이며, 5구의 암면 슬라브 6개를 4줄의 거터에 올려 재배하였다. 전정, 수확 등 작물 관리는 일반적으로 이루어지는 방식으로 작기 내내 진행하였다. 총 96개체의 파프리카를 정식하였고 1주당 2개의 줄기를 V자 형태로 유인하였다. 2020년 6월 3일에 생장점을 제거하였으며, 남은 과실을 수확하고 2020년 7월 7일에 작기를 종료하였다.
2. 데이터 수집 및 전처리
사진은 범용성을 위해 스마트폰(iPhone 11, Apple Inc, CA, USA)으로 촬영하였다. 작물 사진은 2020년 4월 6일부터 6월 24일까지 2-3일 간격으로 촬영하였다 (Fig. 2). 네 거터의 양쪽에서 촬영하여 파프리카의 양면을 각각의 방향에서 이미지에 담았다. 작물의 모습을 전체적으로 담기 위해 바닥에서부터 약 1 m 높이에서 카메라를 들고 위를 향해 사진을 촬영하였으며, 촬영 위치 및 각도의 일관성을 위해 동영상으로 촬영 후 동영상의 프레임을 분할하여 이미지화 하였다. 학습에 사용된 총 이미지 수는 6374장이었으며, 약 70%인 4461장의 이미지를 학습, 약 30%인 1913장의 이미지를 테스트에 이용하였다. 합성곱 신경망의 입력값으로 이미지의 픽셀로 데이터를 사용하였다. 이때, 합성곱 신경망에 입력하기 전 이미지는 0에서 1사이로 정규화되었으며, 고정적인 촬영 방식(매체, 특정 각도, 위치 등)이 재현성에 주는 영향을 줄이기 위해 데이터 증강(data augmentation)을 진행하였다(Simonyan과 Zisserman, 2014).
3. 생체중 회귀식
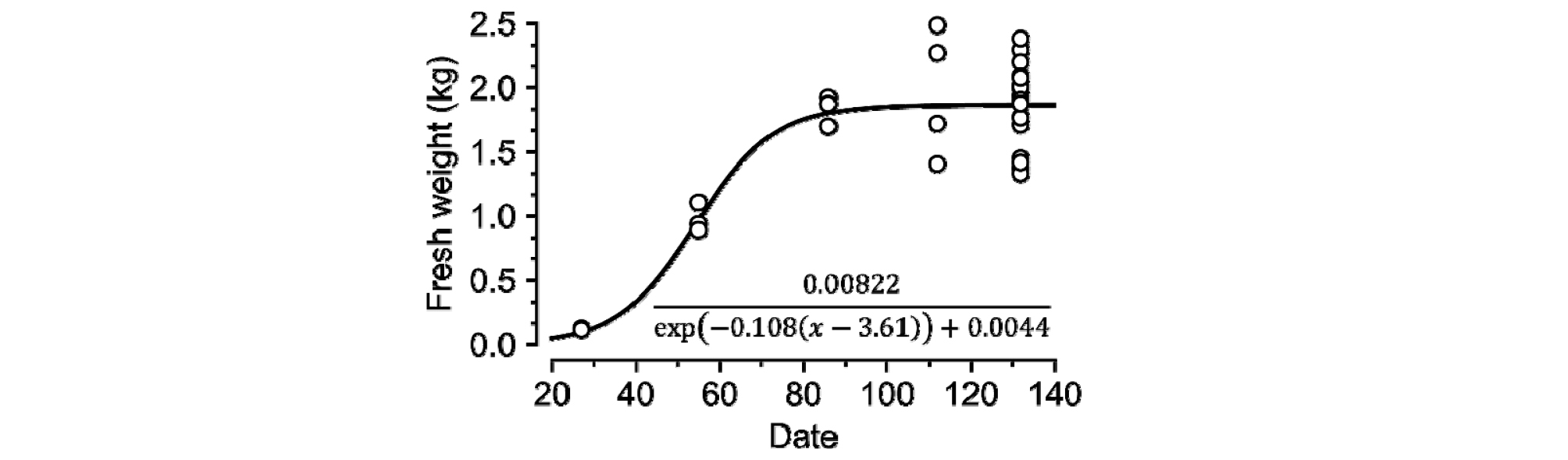
생체중은 정식 후 27, 55, 86, 112, 132일에 파괴조사를 통해 측정하였으며, 정식 후 27, 55, 86일에는 3개체, 정식 후 112일에는 4개체, 작기 종료시점인 정식 후 132일에는 20개체를 임의 추출로 파괴하였다. 파괴조사 시에는 지하부를 제외한 지상부 식물체의 무게를 측정하였다. 측정된 생체중은 시그모이드 함수를 이용하여 회귀 분석하였다(Shi 등, 2016). 회귀된 함수는 이미지가 촬영된 시점에 맞추어 출력값으로 이용되었다.
4. 합성곱 신경망
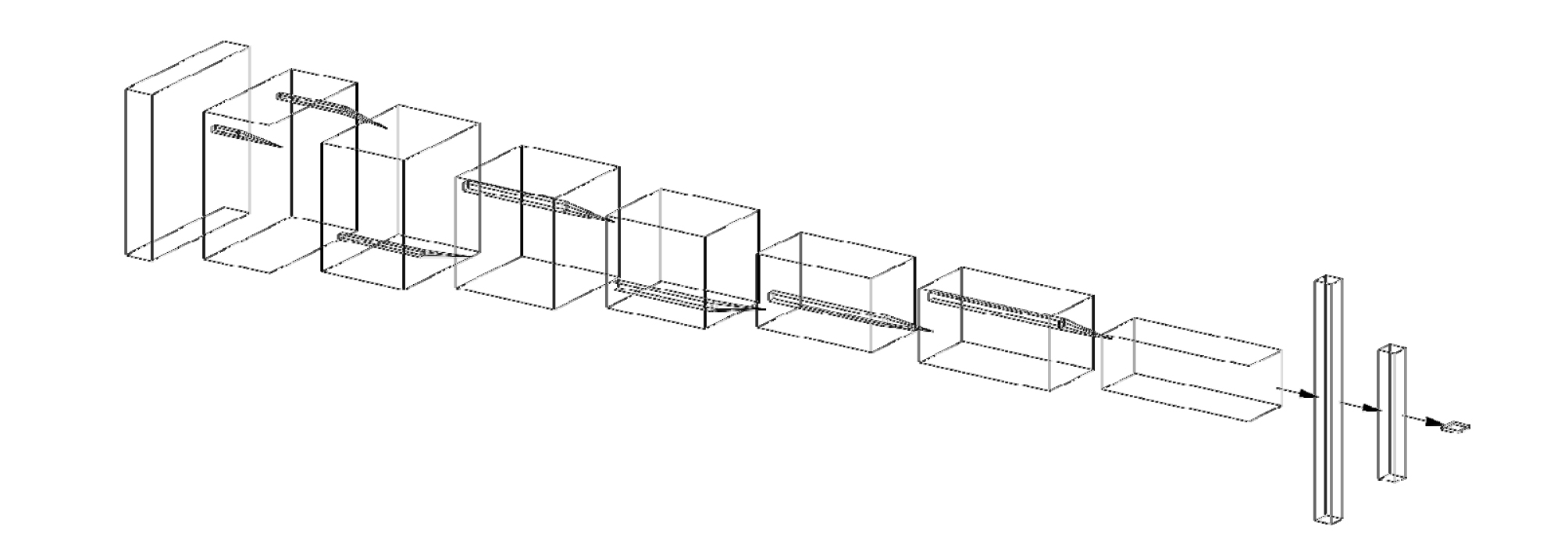
합성곱 신경망은 이미지 픽셀을 입력으로 받아 회귀식에 따른 생체중을 출력하였으며, Tensorflow (v. 2.3.0)을 이용하여 구축하였다(Abadi 등, 2016). 합성곱 신경망은 일반적으로 사용하는 형태로 구축하였다 (Fig. 3). 신경망 구조에 따른 정확도를 알아보기 위해 합성곱 신경망의 구조를 얕은 구조, 깊은 구조, 깊고 채널이 많은 구조로 구축하여 비교하였다(Table 1). 모델 학습은 아담최적화(AdamOptimizer)를 이용해서 추정값과 실측값의 평균오차(MSE)를 최소화하는 방법으로 수행하였다(Kingma와 Ba, 2014). 모델의 정확도 평가하기 위해 결정 계수(R2)와 제곱근 평균오차(RMSE)를 기준으로 사용하였다.
Table 1.
Architectures of the convolutional neural network model used in this study. Layer parameters are denoted as “type of layer” “filter size” “(number of channels)”. Conv2D represents two-dimensional convolutional neural network.결과 및 고찰
1. 생체중 회귀 결과
시그모이드 함수를 이용한 생체중 회귀식은 결정 계수가 약 0.78로 나타났다(Fig. 4). 일반적으로 알려진 바와 같이 성장 후 생체중 증가폭이 줄어드는 형태를 가지며 수렴하였다. 회귀 분석의 특성상 작기 후반부에 드러나는 개체 간 차이는 나타낼 수 없었다. 개체 간 특이성을 나타낼 수 있게 확률 분포까지 고려하고자 한다면 Gaussian process regression (GPR) 등을 활용할 수 있을 것이다(Quinonero-Candela 등, 2007). 결정 계수 0.78은 수용할 수 있는 설명력을 보여주므로, 합성곱 신경망의 출력값으로 이용할 수 있다고 판단하였다.
2. 합성곱 신경망 정확도
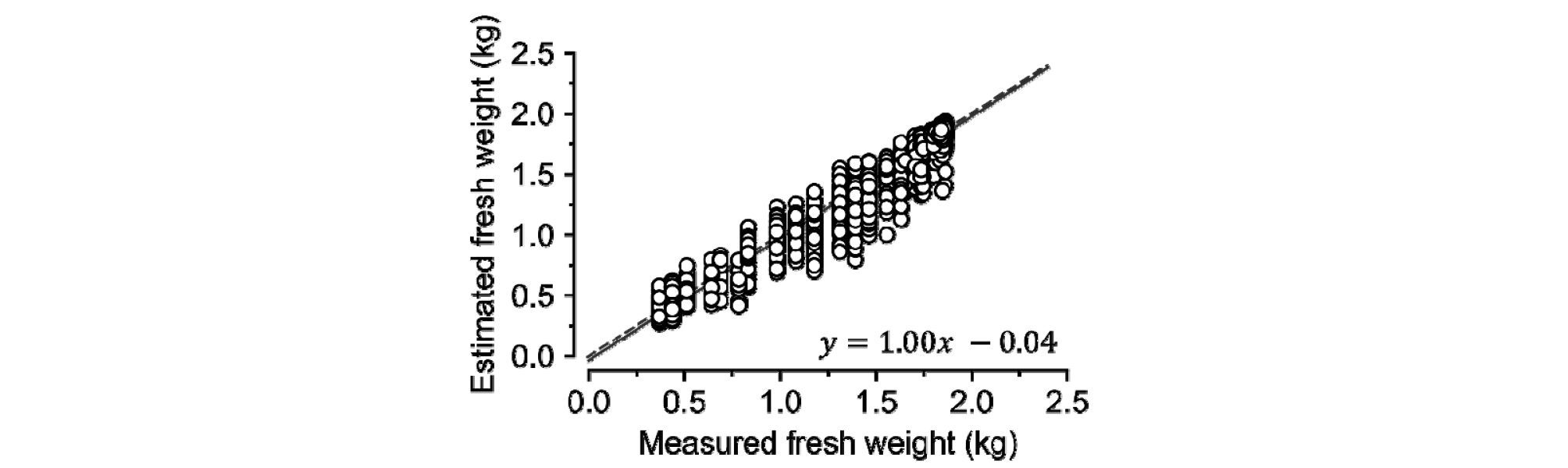
생체중 추정은 깊은 구조에서 최적화되었다(Table 2). 모델 C의 경우 모델 B에서 채널의 수, 즉 학습해야 하는 파라미터의 수를 늘린 형태인데, 모델 B에 비해 파라미터 수는 2배가량 늘어나지만 정확도는 거의 같았다. 따라서, 생체중 추정에 모델 B를 사용하는 것이 적합하다. 그러나, 본 실험에서 사용한 합성곱 신경망들은 현재 알려져 있는 복잡한 모델에 비해서는 비교적 작은 구조이다(He 등, 2016). 합성곱 신경망은 대부분 분류 문제에 사용되었다. 분류 문제의 경우 출력값이 매우 높은 차원을 갖고 있는 경우가 많다(Rawat과 Wang, 2017). 이와 비교하여 본 실험에서 진행한 생체중 추정은 회귀 분석에 가까우므로 더 적은 파라미터가 필요했을 수 있다. 적은 구조임에도 모델이 충분한 정확도를 보여주었으므로, 미가공 데이터 상태의 이미지와 합성곱 신경망은 생체중을 추정하는 데에 사용될 수 있을 것이다.
모델 B의 생체중 추정값은 실제 측정값과 매우 유사한 경향성을 보여주었다(Fig. 5). 회귀선에 비해 추정치가 넓게 분포하고 있지만, 이는 각 이미지에 대해 설정한 출력값이 중복되어 발생한 것으로 보인다. 본 실험에서 입력으로 사용된 이미지는 하루 당 수 백 장에 달한다. 그러나, 생체중은 파괴조사를 시행한 날에만 기록되었으며, 시그모이드 함수로 회귀 분석한 값도 각각의 날에만 해당하는 값이다. 따라서, 다른 형태를 가지고 있는 여러 이미지들이 같은 출력값을 가질 수밖에 없다. 합성곱 신경망 역시 기본적으로 파라미터에 의존하여 움직이기 때문에 서로 다른 입력들이 같은 출력값을 갖더라도 파라미터는 고정되어 있으므로 1:1 그래프 상에서 수직으로 퍼지는 경향을 나타낸 것으로 보인다. 생체중 회귀 함수를 정식 후 날짜가 아닌 시간, 분에 대응하면 서로 다른 출력값을 갖게 할 수 있지만, 파프리카는 매시간 마다 변화가 크게 관찰될 만큼 크게 자라지 않는다(Marcelis와 Ho, 1999). 매 순간의 생체중을 추적할 수 있는 장치를 사용하거나, 출력을 확률 분포로 갖는 신경망 구조를 사용하면 이런 오차를 줄일 수 있을 것이다.
3. 생체중 추정 결과 분석
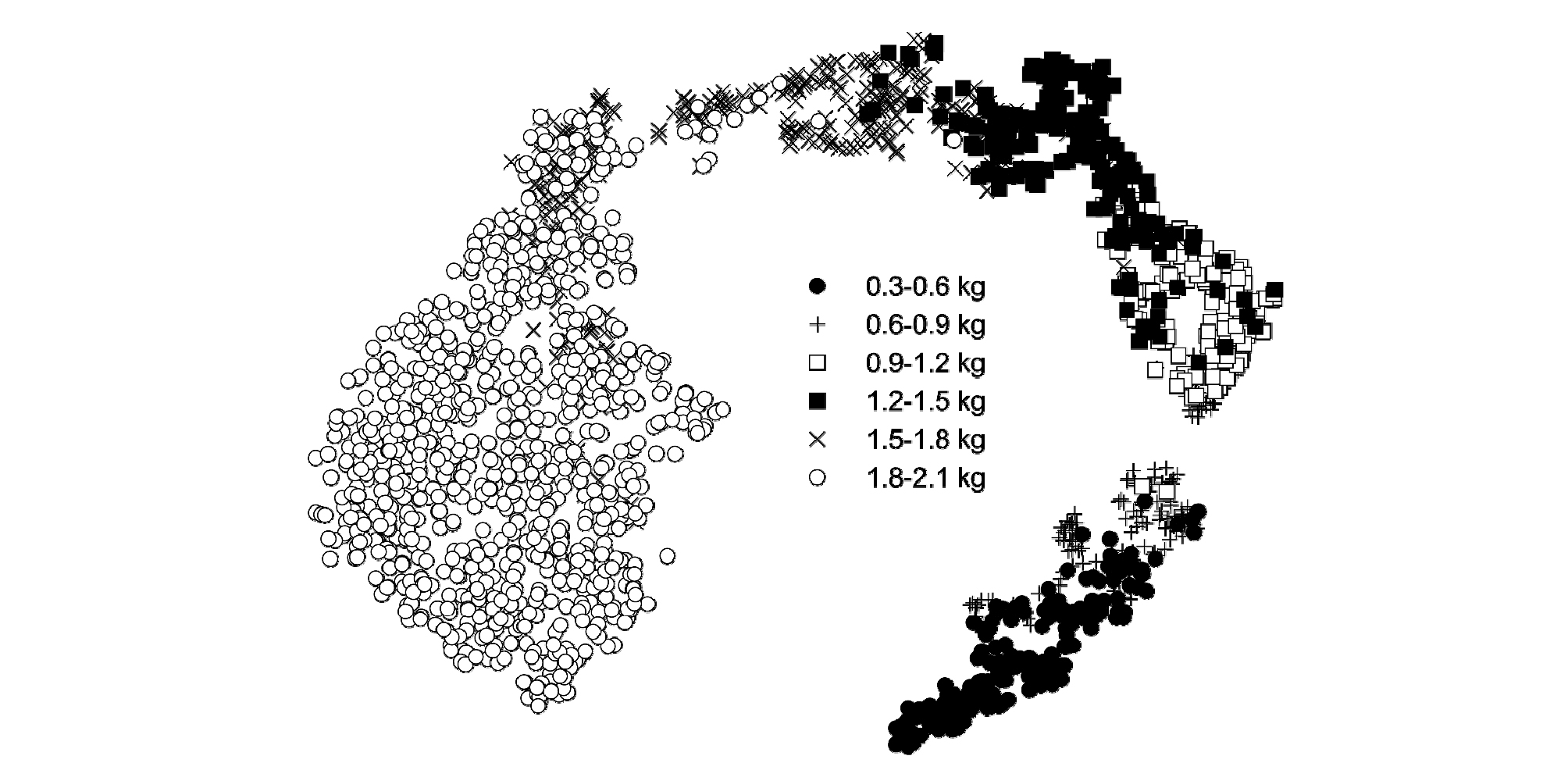
합성곱 신경망이 추정한 이미지들의 2차원 분포를 보면 각 생체중에 해당하는 이미지들이 서로 다른 위치에 분포한 것을 알 수 있다(Fig. 6). 6개 구간으로 나눈 생체중 범위에서 주로 차지한 영역은 서로 다르지만, 경계영역에서 확실하게 분리되지 않고 크게 겹쳐있는 것을 확인할 수 있었다. 겹치는 영역이 있으므로 대략적인 생체중 추정 및 각 이미지에서 생육 변화 양상 확인은 가능하나 각 영역에 해당하는 생체중들을 확실하게 구분하기는 어렵다. 따라서, 본 실험에 사용한 이미지는 정확한 생체중을 확인하기 위해 사용하기는 어렵고, 대략적인 생육 변화 양상을 모니터링하는 용도로 사용하는 것이 적절할 것이다. 확실한 생체중을 추정하려면 생장점 위주로 촬영을 하는 등 촬영 방식을 변경하거나 가시광선 영역 외에 다른 영역도 촬영할 수 있는 초분광영상 기법 등 이미지 자체를 보강하는 방법과 촬영 기간에 수집된 환경 데이터, 무게 측정 데이터 등을 함께 사용하는 방법 등이 있을 것이다.
한편, 2차원 분포가 0.6-0.9kg 부분에서 눈에 띄게 끊어지는 것을 확인할 수 있다. 이는 해당 영역 사이에 특히 구분되는 변화가 있었음을 의미한다. 즉, 생체중이 0.6-0.9kg 사이일 때 이미지에서 드러날 수 있는 작물의 외관 등에서 큰 차이가 났을 것으로 추측할 수 있다. 따라서, 파프리카의 생육 단계를 구분할 때 생체중 0.6-0.9 kg 부근에서 생육 단계 초기와 후기를 구분하는 것이 합리적일 것이다. 이처럼 이미지를 활용한 분포를 분석하면 합리적인 생육 단계를 자동화하는 데 도움이 될 수 있을 것이다.
4. 한계 및 발전 방향
본 실험에서 사용한 이미지 수집 장치는 일반적으로 사용하는 스마트폰이었다. 이는 개발된 모델이 보편적으로 이용될 수 있는 가능성이 있으나, 촬영할 때마다 촬영 방향이 달라지는 등 모델에 혼란을 줄 수 있는 한계점이 있다. 자동으로 특징을 추출하는 CNN의 특성상 촬영 장비에서 생기는 특정한 노이즈를 인식하여 대상을 판별하거나 대상이 아닌 배경의 변화를 인식하여 학습되는 등 원하지 않는 방향으로 학습될 가능성이 있다(Rawat과 Wang, 2017). 데이터 증강을 통해 촬영에 의한 모델의 편향성은 어느 정도 해결할 수 있으나, 모든 환경에 보편적으로 사용한다면 더 많고 다양한 환경에서 데이터를 수집해야 한다. 그러나, 고정된 카메라를 사용하여 데이터를 수집한다면 더 적은 데이터로도 작물의 생체중을 추정할 수 있을 것이다. 또한, 최근 RGB-D 카메라는 가시광선 영역의 이미지 촬영뿐만 아니라 물체의 거리도 인식할 수 있다(Koppula 등, 2013; Chang 등, 2017). RGB-D 카메라를 활용한다면 작물과의 거리를 판단하여 파프리카의 초장, 과실 맺음 여부 등을 함께 알 수 있어 더 정확한 생체중 추정이 가능할 것이다. Support Vector Machine 등 기존에 존재하는 기계학습 방법과의 앙상블 모델 역시 정확도를 높일 수 있을 것으로 예상된다.
또한, 본 실험에서 학습된 모델은 수원의 테스트 베드에서, 파프리카를 재배하는 환경에서 최적화되었다. 따라서, 다른 지역, 다른 온실에서 이 모델을 그대로 사용하거나, 다른 품종 및 색상의 파프리카, 혹은 완전히 다른 작물을 재배하는 환경에서 생체중을 추정하려 한다면 충분한 정확도를 보장할 수 없다(Seginer, 1997). 그러나, 신경망 구조로 대표되는 딥러닝 알고리즘은 유연하게 다른 작업 및 환경에 적용할 수 있으므로, 이후 다른 환경의 온실에서 이미지를 촬영하고 본 실험에서 사용한 데이터와 함께 합성곱 신경망을 학습한다면 보편적인 생체중 추정 모델을 구축할 수 있을 것이다. 이 경우 합성곱 신경망은 사람이 이미지로 생체중을 판단할 때 사용할 수 있는 지표인 길이, 면적, 부피, 밀도값 등을 벗어나 사람이 알지 못하였던 새로운 외적 특징을 추출하여 생체중을 추정할 수도 있다. 따라서, 합성곱 신경망은 기존에 없던 새로운 측정 지표를 제시할 가능성이 있다.
작물 재배에 있어서 생산량은 주요한 목표 중 하나이다. 본 실험에서 합성곱 신경망은 적합한 추정 정확도를 보여주었는데, 딥러닝 모델은 데이터 전처리만 잘 된다면 별다른 수정 없이 적용할 수 있는 유연성이 있다. 데이터만 충족한다면 같은 모델을 재학습하여 생산량을 예측하는 것도 가능할 것이다. 파프리카 생산량일 경우 작물 전체 생체중에서 과실 생체중을 분리하여 학습시키거나, 과실 생체중만 학습시킨다면 재배 시 파프리카 생산량 자체를 추정할 수 있을 것이다. 동시간대 추정이 아니라 향후 생체중에 대한 예측이 필요한 경우에도 데이터 시계열만 달리하여 출력값으로 앞으로의 생체중을 설정하면 모델에 큰 수정 없이 생체중 예측이 가능할 것이다.
또한, CNN 모델의 유연성은 다른 농업 환경에서도 충분히 적용될 수 있는 가능성을 내포한다. 신경망 모델의 유연성은 같은 모델을 다양한 분야에서 인식, 분류, 추론 등 다양한 목적으로 활발히 적용할 수 있는 바탕이 된다(Krizhevsky 등, 2012; Mnih 등, 2015). 따라서, 본 실험에서 학습한 합성곱 신경망도 충분한 데이터와 합리적인 업무를 제공받는다면 다양한 분야에서 같은 형태의 모델을 그대로 사용할 수 있다.